⭐ 9주차 주제: 정렬, BigO [알고리즘]
알고리즘이란?
: 컴퓨터 프로그램이 어떤 문제를 해결하기 위해 필요한 명령어들의 집합
좋은 알고리즘을 찾고 언제 써야 할지 알아야 중요한 프로그램을 만들 수 있습니다.
Ex)
- 구글 행아웃은 어떻게 실시간 영상을 전송하지? 오디오, 비디오 압축 알고리즘을 사용
- 구글 맵스가 어떻게 숙명여대까지의 경로를 찾지? 경로 찾기 알고리즘을 사용
- 픽사는 어떻게 가상 공간에 캐릭터의 3D 모델 조명을 반영해 색칠하지? 렌더링 알고리즘을 사용
- 나사는 태양광 패널을 어디로 언제 움직일지 알까? 최적화 & 스케줄 알고리즘을 사용
정렬
리스트의 항목을 오름차순 또는 내림차순으로 정렬해 놓으면 사람이나 컴퓨터가 리스트에서 어떤 항목을 찾을 때 이진검빠르고 편리하게 찾을 수 있습니다.
정렬하는 방법: 선택 정렬, 버블 정렬, 삽입 정렬, 셸 정렬, 합병 정렬, 퀵 정렬, 힙 정렬, 트리 정렬 등
- 삽입정렬, 선택정렬, 버블정렬 ⇒ 단순해보이지만 비효율적
- 퀵 정렬, 힙 정렬, 합병정렬 ⇒ 복잡해보이지만 효율적

(선택 정렬 알고리즘을 포함하여) 정렬 알고리즘의 중요한 단계는 배열 내 두 개 항목의 위치를 바꾸는 것입니다. -> swap 함수
- 선택 정렬 Selection sort

- 가장 작은 숫자를 찾아서 첫 번째 숫자와 바꿉니다.
- 두 번째로 작은 숫자를 찾아서 두 번째 숫자와 바꿉니다.
- 세 번째로 작은 숫자를 찾아서 세 번째 숫자와 바꿉니다.
- 배열이 정렬될 때까지 그 다음으로 작은 숫자를 올바른 위치로 옮기는 과정을 반복합니다.
따라서 이 알고리즘에서는 다음으로 작은 항목을 선택하고 이를 제자리로 바꾸는 과정을 반복합니다.
- 초기 배열이 [13, 19, 18, 4, 10]인 경우
- 배열 내에서 가장 작은 값의 인덱스를 먼저 찾음
- 4가 가장 작은 값이므로 가장 작은 값의 인덱스는 3
- 선택 정렬은 인덱스 3에 있는 값과 인덱스 0의 값을 바꾸어 [4, 19, 18, 13, 10]가 됩니다. 이제 두 번째로 작은 값의 인덱스를 찾아 이를 인덱스 1의 값과 바꾸기
하위 배열에서의 선택! 가장 작은 값은 이미 인덱스 0과 바뀌었기 때문에 사실은 인덱스 1부터 시작하는 배열의 나머지에서 가장 작은 값을 찾아내야 합니다.
시간 복잡도: O(n^2) 두번의 loop
- 버블 정렬
O(n^2)
list에서 바로 다음에 있는 값과 비교해서 교환하는 방법
숫자의 교체 횟수는 입력 데이터에 의존. 극단적인 경우로 입력 데이터가 우연히 작은 순서대로 나열돼 있을 때는 교체가 한 번도 발생하지 않으나 반대로 숫자가 큰 순서대로 나열돼 있으면 비교할 때마다 계속 교체해 주어야 합니다.

- 삽입 정렬 Insertion Sort
O(n^2)
삽입 정렬은 1번 인덱스 부터 n-1 사이에 있는 배열의 따라 순환하며 알맞은 자리를 찾는 방법입니다.
중요한 점! 첫번째 요소를 오른쪽으로 한 칸 움직일 수 있는 slide 기능이 있어야 하고, 둘째로 key가 그 바로 왼쪽에 있는 요소로 치환되지 않도록 이 key를 보관하는 공간이 필요합니다.
삽입 정렬의 주요 단계는 배열에 key변수에 저장된 값을 넣기 위한 공간을 만드는 것 입니다. 삽입 정렬은 key의 초기 위치에서 왼쪽에 있는 하위 배열을 오른쪽에서 왼쪽으로 가면서 key보다 값이 더 큰 요소를 오른쪽으로 하나씩 밀어가면서 정렬합니다.

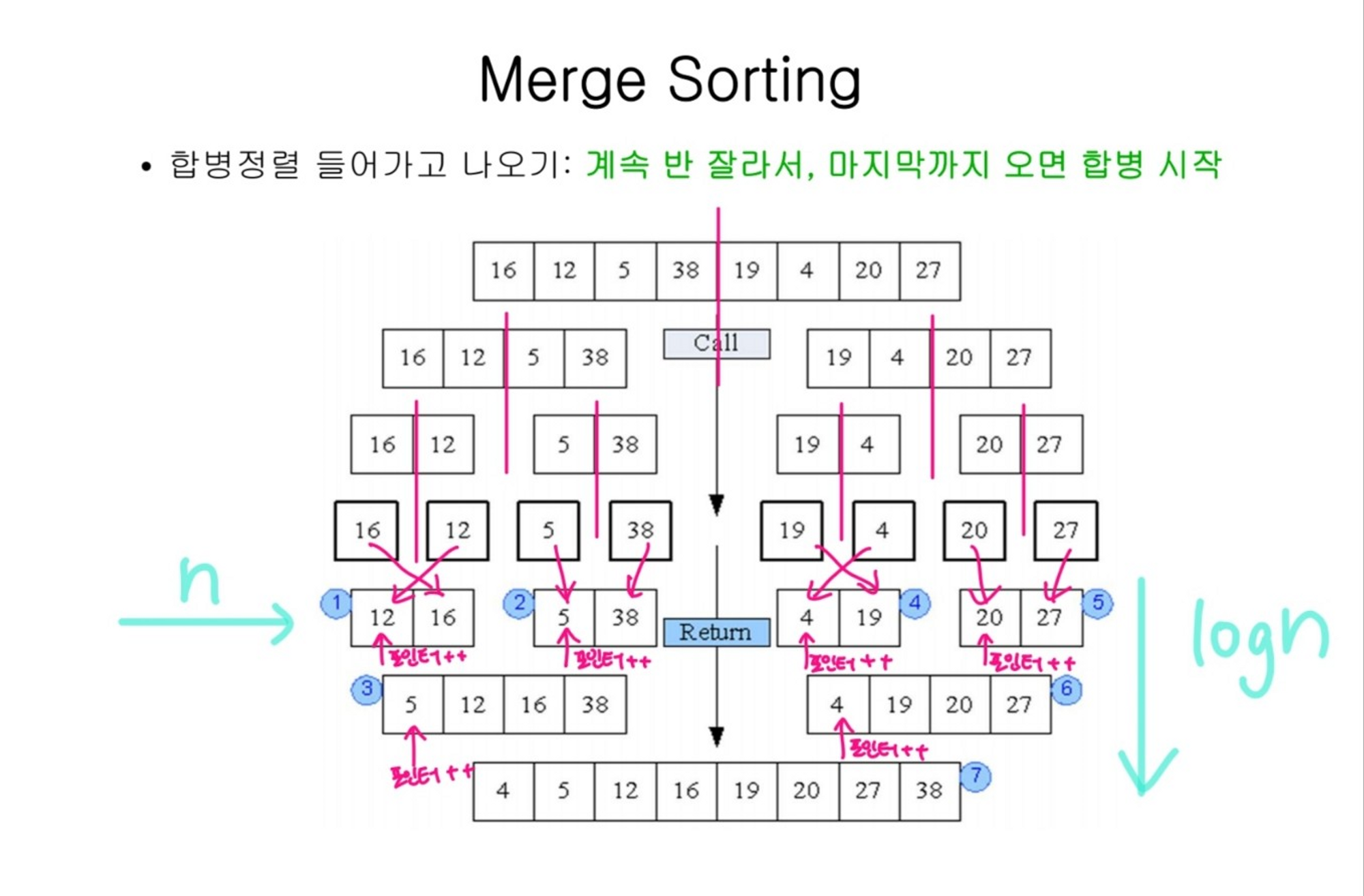
- 합병 정렬 Merge Sorting
O(nlogn) 위의 n^2보다 성능이 좋음

- 퀵 정렬 Quick sort
O(nlogn)
퀵 정렬 알고리즘은 다른 알고리즘에 비해 자료들을 서로 비교하고 교환하는 횟수가 적다는 장점을 가지고 있음 ⇒ 이는 수행 시간의 단축으로 이어지게 되고, 이는 자료를 관리하는 데 있어 필수적, 따라서 대용량 데이터베이스 처리 시스템 등 다양한 분야에서 활용되고 있습니다.
오름차순으로 정렬할 때 어떠한 자료를 기준으로 작거나 같은 값을 지닌 자료는 앞으로, 큰 값을 지닌 자료는 뒤로 가도록 하여 작은 값을 갖는 데이터와 큰 값을 갖는 데이터로 분리해가며 정렬하는 방법
퀵 정렬은 합병정렬과 비슷하게 분할정복(Divide and Conquer) 알고리즘!
분할 정복 알고리즘의 하나로, 평균적으로 매우 빠른 수행 속도를 자랑하는 정렬 방법
합병 정렬(merge sort)과 달리 퀵 정렬은 리스트를 피벗을 기준으로 비균등하게 분할합니다.
자료들을 작은 2개의 자료로 분리하고 각각을 해결한 다음, 결과를 모아서 원래의 문제를 해결하는 전략이다. 분할 정복 방법은 대개 순환 호출을 이용하여 구현합니다.
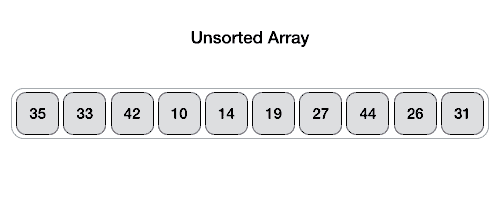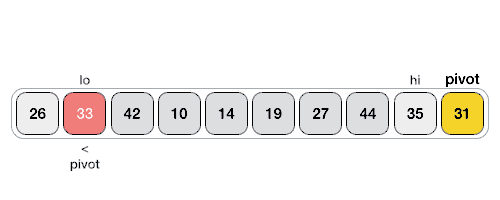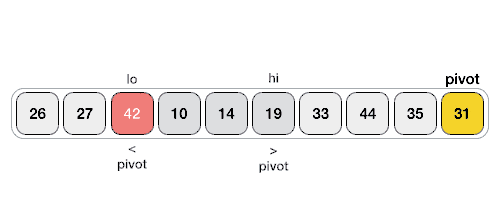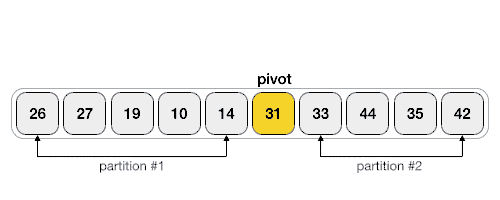
이 Pivot 값을 기준으로 오름차순 정렬을 가정 시, Pivot 보다 작은 값은 왼쪽에, Pivot 보다 큰 값은 오른쪽에 위치시키는 방식을 활용!
1회의 작업이 완료되면 좌측 / 우측의 정렬이 완료되지 않은 부분 집합이 형성되고 그러면 그 부분 집합 내에서 또 다시 Pivot 값을 하나 선정하고 같은 정렬을 반복하는 것입니다.
위와 같이 큰 문제를 지속적으로 작은 문제로 나누어 해결하는 방식을 취하기 때문에 퀵 정렬도 이전 포스팅의 병합 정렬과 같이 **분할 정복 알고리즘(Divide and Conquer Algorithm)**입니다.
- 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 pivot(피벗) 이라고 한다.
- pivot을 기준으로 pivot보다 작은 요소들은 모두 pivot의 왼쪽으로 옮기고 pivot보다 큰 요소들은 모두 pivot의 오른쪽으로 옮긴다.
- pivot을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
3-1) 분할된 왼쪽 리스트와 오른쪽 리스트도 다시 pivot을 정하고 pivot을 기준으로 2개의 부분리스트로 나눈다.
3-2) 재귀를 사용하여 부분 리스트들이 더이상 분할이 불가능 할 때까지 반복한다.
- 퀵정렬은 최악의 경우 pivot이 배열 내에서 가장 작은 값 또는 가장 큰 값으로 설정된다면 원소 n개에 대해서 n번, (n-1)번, (n-2)번...1번 의 비교가 필요하므로 시간 복잡도가 O(n^2)
- **평균 시간 복잡도는 O(nlogn)**으로 빠르다. pivot 값이 적절히 설정된다면 그 속도가 매우 빠르다. 따라서 pivot값을 잘 설정하는 것이 중요하다.
놀라운 점! Pivot 결정하기

Pivot이 적당히 중간 즈음 위치했다면 양 쪽의 부분 집합이 균등하게 배분되어 전체 비교 횟수를 현저히 줄일 수 있는데 이와 같은 현상이 반복된다면 비교를 더욱 많이 해야 합니다. 사실상 버블 정렬과 다를 바가 없다…! 이런 최악의 경우, 전체 시간 복잡도는 O(n^2) 만큼 발생하게 되어 퀵 정렬의 장점이 사라집니다.
① 그냥 Random하게 골라보기
랜덤하게 설정하면 항상 최악의 Case가 되지는 않을 것. 그러나 최악의 Case가 생겨날 수는 있다. (평균적으로 O(nlogn) 유지)
② Median-Of-3 method
이는 배열의 값들 중 가장 좌측 / 우측, 중앙값 3개를 뽑고, 그 3개의 값을 우선적으로 정렬한 뒤, 그 중 중간 값을 가장 좌측 또는 우측으로 이동시켜 Pivot으로 설정한 뒤 퀵 정렬을 수행하는 방법이다.
이 값이 Pivot으로 사용되어 전체 배열을 균등하게 분할할 것이라는 보장은 없지만, 최소한 이 값이 전체 값 중 최대 / 최소값에는 해당하지 않기 때문에 중심 극한 정리에 따라 평균적으로 O(nlogn)의 시간복잡도를 유지할 수 있게 된다.
BigO
점근적 표기법
알고리즘의 실행 시간은 컴퓨터가 알고리즘 코드를 실행하는 속도에 의존합니다.
이 속도는 컴퓨터의 처리속도, 사용된 언어 종류, 프로그래밍 언어를 컴퓨터가 실행할 수 있는 코드로 바꾸는 컴파일러의 속도 등에 달려있습니다.
우선, 입력값의 크기에 따른 알고리즘의 실행 시간을 알아야 합니다. 배열의 크기가 커지면 선형 검색과 이진 검색의 최대 추측 횟수가 함께 증가하듯이. 예를들어 GPS가 모든 골목길이 아니라 고속도로만 찾으면 길을 훨씬 금방 찾을 수 있을겁니다. ⇒ 입력값의 크기에 대한 함수로 알고리즘 실행 시간을 생각할 수 있습니다.
점근적 표기법(asymptotic notation) - 점근(漸近)이란 점점 가까워 지는 모양을 뜻합니다.
중요하지 않은 항과 상수 계수를 제거하면 이해를 방해하는 불필요한 부분이 없어져서 알고리즘의 실행 시간에서 중요한 부분인 위에서 예시를 든 시간 성장률에 집중할 수 있습니다. 상수 계수와 중요하지 않은 항목을 제거하여 불필요한 부분은 버리고 가장 중요한 부분만 추려내서 함수를 간소화해야 합니다.
- 최고차항을 제외하고 모두 생략한다.
- 최고차항에 붙어있는 계수들을 모두 생략한다.
보통 상수 인자와 낮은 차원의 항목은 생략하고 사용합니다. 이제 점근적 표기법의 세 가지 형태를 살펴봅시다. 바로 big-Θ, big-O, big-Ω 표기법입니다.
Time complexity: 복잡한 로직 처리를 했을 때 얼마의 시간이 걸리는가?
Big-O (빅 오)
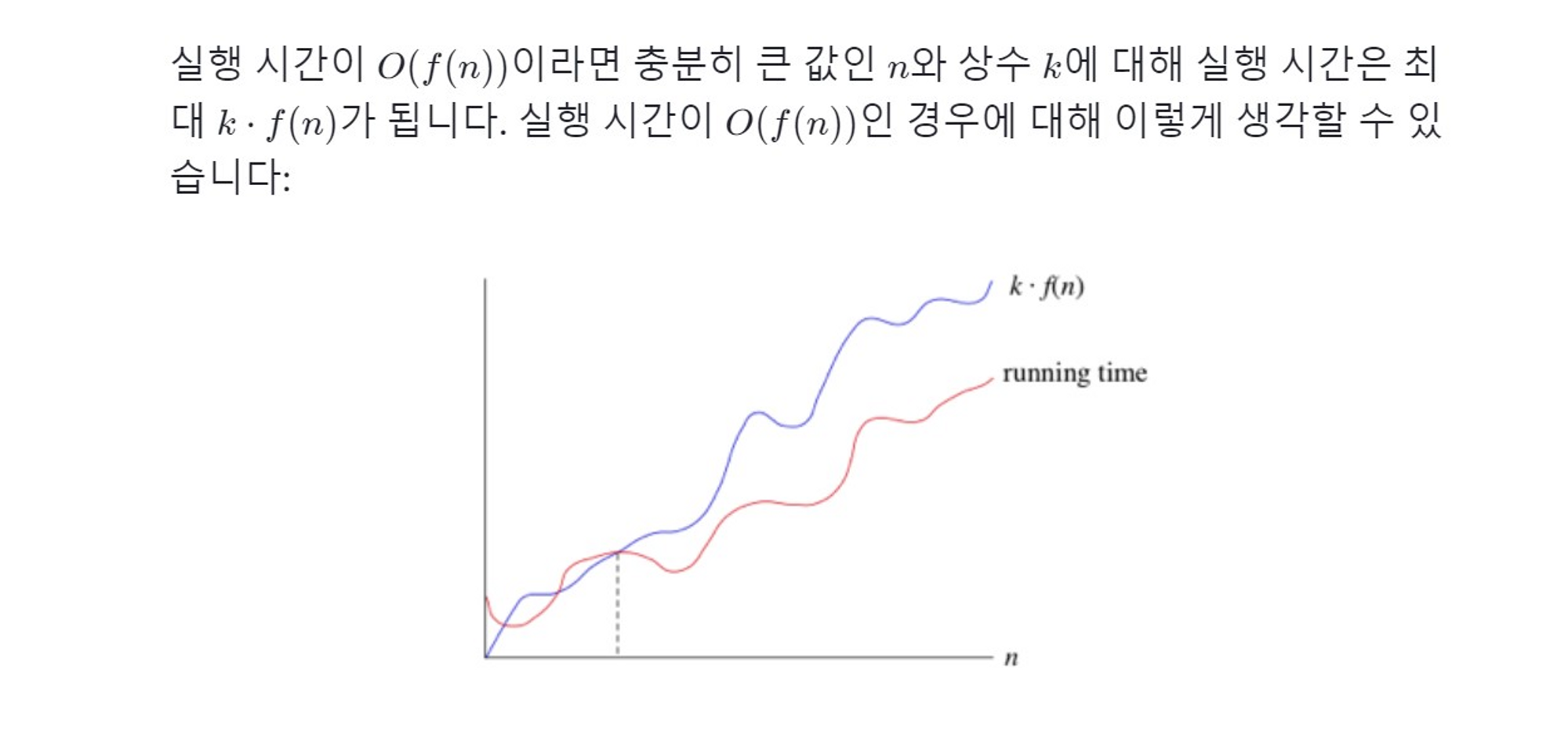
“실행 시간은 최대한 이만큼 커지지만 더 천천히 커질 수도 있다"는 의미인 점근적 표기법 형태를 사용하는 것이 편리할 수도 있습니다. 이런 경우를 위해 "big-O" 표기법을 사용합니다.
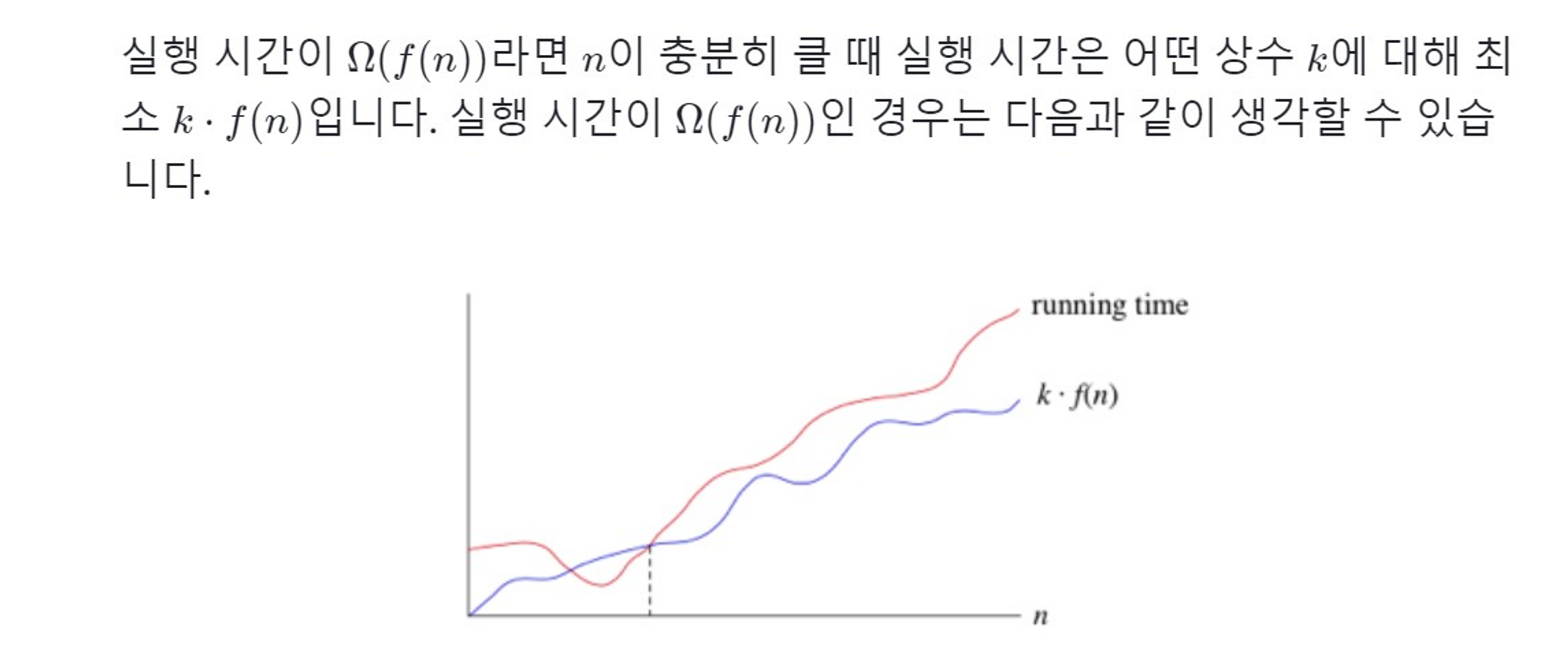
Big-Ω (빅 오메가)
때로는 알고리즘이 상한선 없이 최소한 어느 정도 걸린다고 해야 할 때 필요합니다.
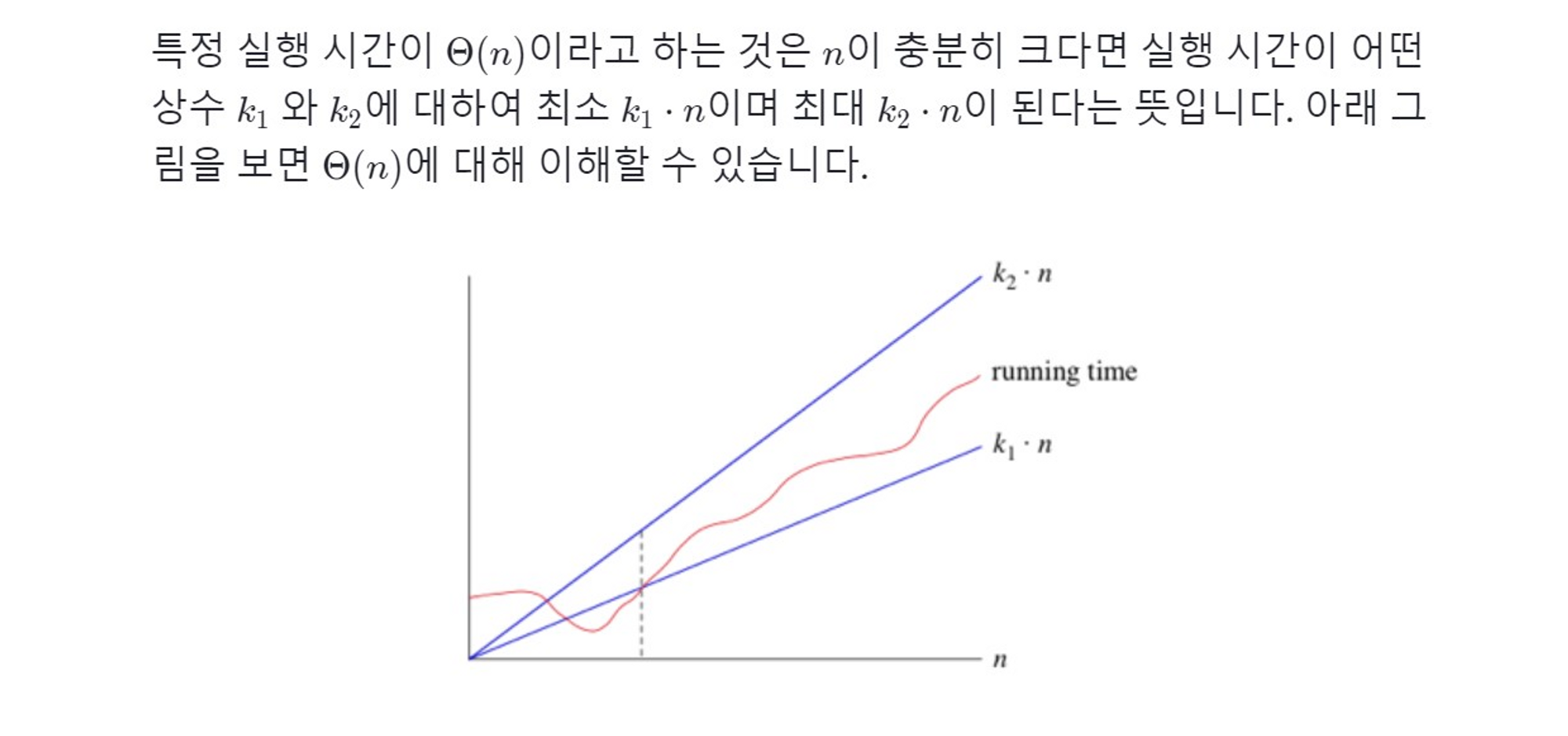
Big-θ (빅 세타)
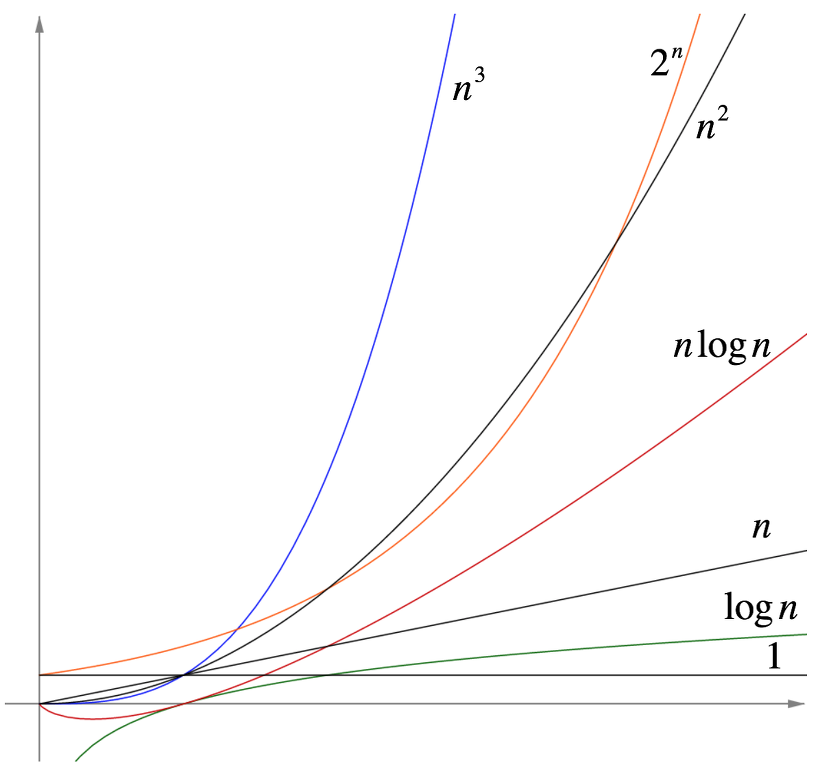
Quiz
- 합병정렬 과 쾌속정렬 비교 - 합병정렬은 최악의 경우에도 O(nlogn)을 보장하지만 퀵소트 즉, 쾌속정렬은 최악의 경우 O(N^2)이 되기도 합니다. 그런데 퀵소트가 빠른 이유는 임시저장공간이 필요한 합병정렬과 달리 임시저장공간이 필요없어서 옮기고 가져오는데에 시간이 필요하지 않기 때문에 평균적으로 쾌속정렬이 빠릅니다.
- 빅오, 빅쎄타, 빅오메가 들의 차이를 설명하세요.
- 빅오 계산법에 대해 설명하시오
- 빅오 표기법은 보통 알고리즘의 시간 복잡도와 공간 복잡도를 나타내는데 주로 사용 되며 필요한 계산 횟수를 정확한 숫자로 표현하느 것이 아니라 입력 크기와의 관게로 표현한다
- 퀵 정렬 방법에 대해 설명하시오
- 리스트 안에 있는 한 요소를 선택한다. 이렇게 고른 원소를 피벗(pivot) 이라고 한다.
- 피벗을 기준으로 피벗보다 작은 요소들은 모두 피벗의 왼쪽으로 옮겨지고 피벗보다 큰 요소들은 모두 피벗의 오른쪽으로 옮겨진다. (피벗을 중심으로 왼쪽: 피벗보다 작은 요소들, 오른쪽: 피벗보다 큰 요소들)
- 피벗을 제외한 왼쪽 리스트와 오른쪽 리스트를 다시 정렬한다.
- 분할된 부분 리스트에 대하여 순환 호출 을 이용하여 정렬을 반복한다.
- 부분 리스트에서도 다시 피벗을 정하고 피벗을 기준으로 2개의 부분 리스트로 나누는 과정을 반복한다.
- 부분 리스트들이 더 이상 분할이 불가능할 때까지 반복한다.
-
- 여러 정렬 방법중 가장 효율적인 정렬은 무엇인가?
- 답 최선의 경우 평균적인 경우 최악의 경우
삽입정렬 O(N) O(N^2) O(N^2) 퀵 정렬 O(NlogN) O(NlogN) O(N^2) - 퀵정렬. 아래의 표와 같이 평균적인 경우를 고려했을때 가장 시간 복잡도가 낮음
- Big O의 필요성
- 답처리 속도, 메모리등은 하드웨어의 스펙에 의해서 좌지우지되지만 처리단계는 하드웨어와 상관없이 일정하다.
- 정량적으로 알고리즘의 성능을 판단하기 위한 기준으로서 필요.
Q. 퀵 정렬의 장점과 단점이 무엇인가?
A. 장점은 속도가 빠르고, 추가적인 메모리 공간을 필요로 하지 않는다.
단점은 정렬된 배열에 대해서는 오히려 수행시간이 더 걸리게 되는 것이다.
- 피봇을 가장 앞에 위치하는 원소로 잡는다면 분할 과정에서 피봇값보다 작은 값은 없기에 비대칭 적인 파티션으로 나누어지게 된다. 이런 방식으로 피봇을 계속 설정하면 분할이 일어날 때마다 비대칭적인 파티션으로 나뉘기 때문에 시간복잡도가 O(n^2)이 되어 수행시간이 일반적인 경우보다 훨씬 길어지게 된다.
[출처] 정렬(버블 정렬, 선택 정렬, 삽입 정렬, 힙 정렬, 병합 정렬, 퀵 정렬)|작성자 kimsehi1
[출처] [Algorithm] 알고리즘 - 시간 복잡도의 점근적 표기, 빅오(big-O)|작성자 넬티아
[네이버 지식백과] 퀵 정렬 알고리즘 - 빠르게 정렬하는 알고리즘 (소프트웨어 알고리즘, 안성진, 고근호)
[출처] https://gmlwjd9405.github.io/2018/05/10/algorithm-quick-sort.html