이 노트는 SMUPC에 참가하시는 분들을 위해 작성한 글입니다. Python, C, C++, Java 코드가 작성되어 있으니 대회 문제를 푸실 때 많은 도움이 되기를 바랍니다. 오타나 오류가 있을 수 있다는 점... 감안하시고 봐주시면 감사하겠습니다:)
SMUPC 참가하시는 분들 모두 화이팅!

목차
1. 시간복잡도
2. 정렬
3. Stack, Queue
4. 이진검색, 이분탐색
5. DFS, BFS
시간 복잡도
- 문제를 해결하는데 걸리는 시간으로 주로 Big-O 표기법을 사용한다.
- Big-O 표기법은 계수와 낮은 차수의 항을 제외한다.
- 알고리즘 문제를 풀기 전에 생각한 풀이가 제한된 시간 복잡도를 넘지는 않는지, 문제를 풀고 난 후에는 제한된 시간 복잡도에 맞게 풀었는지 확인하는 데 중요한 개념이다.
O(1)
- 상수 시간
- 입력값과 상관없이 단 한번의 연산만 수행하므로 시간이 늘어나지 않는다. 배열의 길이와 상관 없이 즉시 값을 출력할 수 있기 때문이다.
- 아래 함수에서 print문이 2번 반복되더라도 O(2)가 아닌 O(1)임을 헷갈리지 말자
- O(1)은 몇 백번 반복되더라도 O(1)
array=[1,3,3,7]
def print_one(array):
print(array[1]);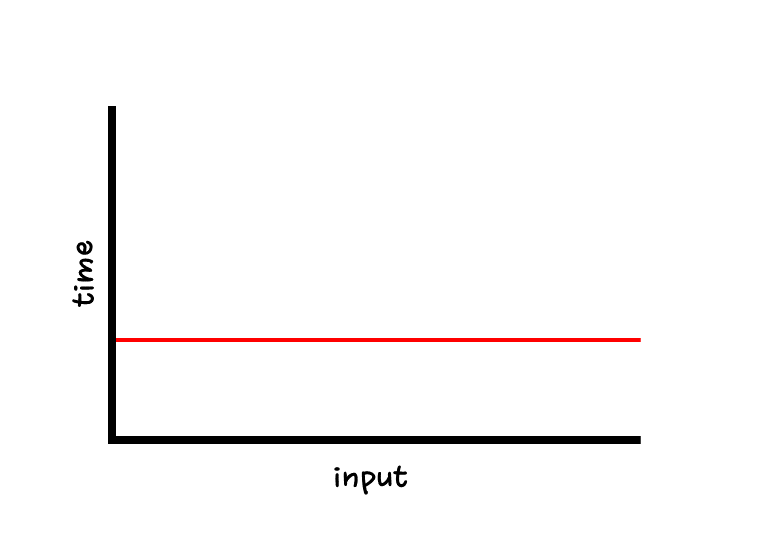
O(N)
- 선형 시간
- 아래 함수에서 입력된 배열의 길이가 4이면 4번을 출력하고 100이면 100번을 출력하듯이 선형적으로 증가한다.
- 배열의 길이가 N이면 nN만큼 반복하여 출력하므로 O(N)이다.
- O(N) 역시 for문이 끝나고 또 for문이 시작해도 O(2N)이 아닌 O(N)이다.
- 간단히 생각하자면 for문이 몇 번 반복되는 지 세보면 된다.
array=[1,3,3,7]
def print_one(array):
for i in array:
print(i)
O(N^2)
- 2차 시간
- 중첩이 있을 경우 발생한다.
- 아래 함수를 보면 i가 0일 때 j가 4번 반복하고, i가 1일 때 j가 다시 4번 반복하고... 결론적으로 4*4번 반복한다.
- 따라서 아래 함수의 시간복잡도는 O(N^2)이다.
array=[1,3,3,7]
def print_one(array):
for i in array:
for j in array:
print(i,j)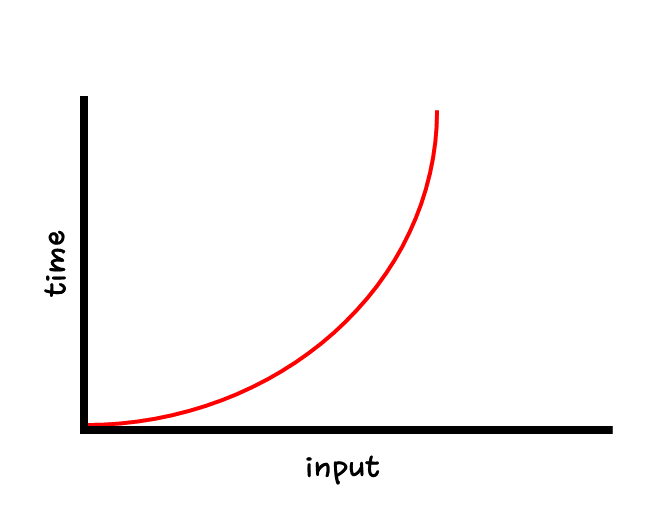
O(logN)
- 로그 시간
- 주로 이진 검색할 때 사용한다.
- 이진 검색은 배열을 간단히 설명하자면 정렬된 길이 10의 배열이 있을 때 특정 수를 찾는다고 해보자. 이 수를 빠르게 찾기 위해 배열을 반으로 나누면서 찾아가기에 빠르게 검색할 수 있고 이 작업이 O(logN)만큼 걸린다.
- 로그의 밑 지수는 2이다.
16을 2로 나누면 8
8을 2로 나누면 4
4를 2로 나누면 2
2를 2로 나누면 1
따라서 특정 값을 찾는데 4번이면 가능하다.
log16=4이므로 이진 검색하는 데 O(logN)만큼 걸린다.

정렬
데이터를 오름차순, 내림차순 등으로 나열하는 알고리즘
Python
리스트에 사용 가능하며 list.sort() 형식으로 사용한다.
list=[1,4,6,2,10,20,2,3]
//오름차순
list.sort()
//[1,2,2,3,4,6,10,20]
//내림차순
list.sort(reverse=True)
//[20,10,6,4,3,2,2,1]C
기본 구조
void qsort (void *base, size_t num, size_t size, int (*compare)(const void *, const void *);- base: 정렬하고자 하는 배열
- num: 배열의 원소의 총 개수
- size: 배열의 원소 하나의 크기
- compare: 특정 조건을 추가하고 싶을 때 사용하는 함수
- 오름차순 정렬
- 첫 번째 변수 > 두 번째 변수 일 때 1 반환
- 첫 번째 변수 < 두 번째 변수 일 때 -1 반환
- 첫 번째 변수 == 두 번째 변수 일 때 0 반환
- 내림차순 정렬
- 첫 번째 변수 < 두 번째 변수 일 때 1 반환
- 첫 번째 변수 > 두 번째 변수 일 때 -1 반환
- 첫 번째 변수 == 두 번째 변수 일 때 0 반환
- 꼭 1, -1 일 필요없이 양수와 음수로도 구별할 수 있다.
- 오름차순 정렬
#include<stdio.h>
#include<stdlib.h>
int static compare (const void* first, const void* second)
{
if (*(int*)first < *(int*)second)
return 1;
else if (*(int*)first > *(int*)second)
return -1;
else
return 0;
}
int main(){
int arr[] = {5,3,8,10,1};
int arr_size = sizeof(arr) / sizeof(int);
int i;
//오름차순 정렬
qsort(arr, arr_size, sizeof(int));
//[1,3,5,8,10]
//내림차순 정렬
qsort(arr, arr_size, sizeof(int), compare);
//[10,8,5,3,1]
return 0;
}C++
sort(배열의 시작 주소, 배열의 시작 주소+배열의 크기, [비교함수]) 형식으로 사용한다
비교함수의 경우에는 특정 조건을 기준으로 정렬하고 싶거나 내림차순으로 정렬하고 싶을 때 사용한다.
#include<iostream>
#include<algorithm>
using namespace std;
bool cmp(int a, int b){
return a>b;
}
int main(){
int arr[5]={4,7,1,9,3};
//오름차순 정렬
sort(arr, arr+5);
//{1,3,4,7,9}
//내림차순 정렬
sort(arr, arr+5, cmp);
//{9,8,4,3,1}
//인덱스 1부터 3까지 정렬
sort(arr+1, arr+3);
//{4,1,7,9,3}
return 0;
}Java
int[] arr={5,7,3,10,1};
//오름차순
Arrays.sort(arr)
// {1,3,5,7,10}
//내림차순
import java.util.Collections;
Arrays.sort(arr, Collections.reverseOrder());
//{10,7,5,3,1}STACK, QUEUE
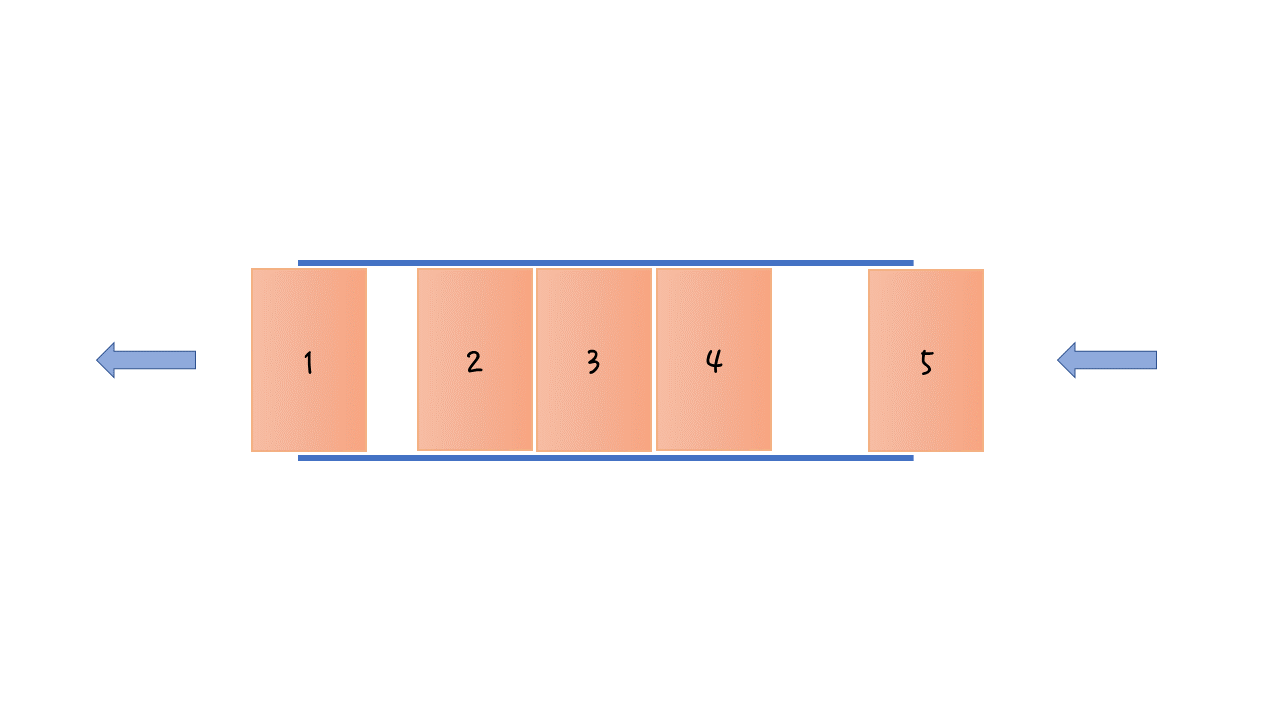
스택
- 한 쪽 끝에서만 원소를 넣고 빼는 구조
- LIFO(Last In First Out): 나중에 들어온 것이 먼저 나감
- 보통 제일 위에 있는 원소를 top이라 한다.

큐
- 한 쪽으로는 원소를 넣고 다른 쪽으로 빼는 구조
- FIFO(First In First Out): 먼저 들어온 것이 먼저 나감
- 보통 제일 먼저 나가는 원소를 front, 제일 나중에 들어온 원소를 rear라고 한다.
Python
스택
- python에는 스택 함수가 따로 없어서 직접 구현하거나 deque 라이브러리를 스택 대신 사용한다.
- deque는 간단하게 설명하자면 양방향으로 삽입, 제거가 가능하다.
- deque의 오른쪽을 스택의 top 부분이라 생각하면 아래와 같이 사용할 수 있다.
from collections import deque
dq=deque() # 덱 생성
dq.append() # 가장 오른쪽에 원소 삽입
dp.pop() # 가장 오른쪽의 원소 반환
dp.clear() # 모든 원소 제거큐
- 큐 역시 deque 라이브러리를 대신 사용할 수 있다.
- 오른쪽이 원소가 들어오는 쪽이고 왼쪽이 나가는 쪽이라 해볼 때 코드는 아래와 같다.
from collections import deque
dq=deque() # 덱 생성
dq.append() # 가장 오른쪽에 원소 삽입
dq.popleft() # 가장 왼쪽의 원소 반환
dp.clear() # 모든 원소 제거C
스택
- C는 스택 라이브러리가 없기 때문에 배열을 통해 직접 구현해야한다.
#include<stdio.h>
#define SIZE 5
//배열로 스택 선언
int stack[size];
int top=-1; //제일 나중에 들어온 원소의 위치
int isEmpty(){
if(top == -1){
printf("ERROR: Stack is empty!\n");
return 1;
}
return 0;
}
int isFull(){
if(top > SIZE){
printf("ERROR: Stack is Full!\n");
return 1;
}
return 0;
}
void push(int x){
if(!isFull()){ //꽉 차있지 않으면
top++; //제일 위에 있는 원소가 바뀜
stack[top] = x;
}
}
int pop(){
if(!isEmpty()){ //비어있지 않으면
return stack[top--]; //원소 한 개를 빼므로 top이 하나 줄어들음
}
}
int main(){
push(1); //[1]
push(2); //[1,2]
push(3); //[1,2,3]
pop(); //[1,2]
pop(); //[1]
return 0;
}큐
- 큐도 라이브러리가 없기 때문에 배열로 직접 구현해야 한다.
#include<stdio.h>
#define SIZE 5
//배열로 큐 선언
int queue[size];
int front=0; //제일 먼저 들어온 원소의 위치
int rear=-1; //제일 나중에 들어온 원소의 위치
int isEmpty(){
if(front==rear){
printf("ERROR: Queue is empty!\n");
return 1;
}
return 0;
}
int isFull(){
if((rear+1)%SIZE==front){
//index가 0에서 시작하기 때문에 rear+1을 큐의 사이즈로 나눴을 때 front와 같으면 큐가 꽉 차있음
printf("ERROR: Queue is Full!\n");
return 1;
}
return 0;
}
void push(int x){
if(!isFull()){
rear++;
stack[rear] = x;
}
}
int pop(){
if(!isEmpty()){
return stack[front++];
}
}
int main(){
push(1); //[1]
push(2); //[1,2]
push(3); //[1,2,3]
pop(); //[2,3]
pop(); //[3]
return 0;
}C++
스택
- 헤더: #include<stack>
- 선언: stack<데이터타입>이름
스택 기본 함수
- push(a): stack에 a 추가
- pop(): 제일 마지막에 추가된 원소 제거
- top(): 제일 마지막에 추가된 원소 반환
- empty(): stack이 비어있으면 true, 아니면 false 반환
- size(): stack에 들어있는 원소의 개수 반환
#include<iostream>
#include<stack>
using namespace std;
stack<int>s;
int main(){
s.push(1); //s={1}
s.push(2); //s={1,2}
s.push(3); //s={1,2,3}
s.pop(); //s={1,2}
cout<<s.top()<<'\n'; //2
cout<<s.empty()<<'\n'; //0
cout<<s.size()<<'\n'; //2
return 0;
}큐
- 헤더: #include<queue>
- 선언: queue<데이터타입>이름
기본 함수
- push(a): queue에 a 추가
- pop(): 제일 먼저 추가된 원소 제거
- front(): 제일 먼저 추가된 원소 반환
- back(): 제일 나중에 추가된 원소 반환
- empty(): queue가 비어있으면 true, 아니면 false 반환
- size(): queue에 들어있는 원소의 개수 반환
#include<iostream>
#include<queue>
using namespace std;
queue<int>q;
int main(){
q.push(1); //q={1}
q.push(2); //q={1,2}
q.push(3); //q={1,2,3}
q.front(); //1
q.back(); //3
q.pop(); //q={2,3}
cout<<q.empty()<<'\n'; //0
cout<<q.size()<<'\n'; //2
return 0;
}Java
스택
import java.util.Stack
Class Main{
Stack<Integer>s =new Stack<Integer>();
public static void main(){
s.push(1); //데이터 삽입
s.peek(); //top 데이터 참조
s.pop(); //top 데이터 반환
s.claer(); //초기화
s.size(); //스택안에 있는 요소의 개수 반환
s.empty(); //스택이 비어있다면 true, 아니면 false 반환
s.contains(1); //스택에 1이 있으면 true, 아니면 false 반환
}
}큐
import java.util.Queue;
import java.util.LinkedList;
Class Main{
Queue<Integer>q=new LinkedList<>();
public static void main(){
q.add(1); //1 삽입
q.add(2); //2 삽입
q.offer(3); //3 삽입
q.poll(); //첫번째 원소 반환 후 삭제
q.peek(); //첫번째 원소 참조
q.remove(); //첫번째 원소 삭제
q.clear(); //초기화
q.size(); //큐 원소의 개수
q.contatins(3); //큐가 3을 포함하면 true, 아니면 false 반환
}
}
이진검색, 이분탐색
이분탐색은 정렬되어 있는 리스트에서 탐색 범위를 절반씩 줄여가며 원하는 데이터를 탐색하는 알고리즘이다.
정렬된 리스트에서 중간 값을 선택하고 선택한 값과 찾고자 하는 값의 크고 작음을 비교한다. 선택한 중간값이 만약 찾는 값보다 크면 그 값은 새로운 최댓값이 되며, 작으면 그 값은 새로운 최솟값이 된다.
꼭 정렬해야함을 잊지 말자!
Python
def binarySearch(array, target, low, high):
if low > high:
return False
mid = (low+high) / 2
if array[mid] > target:
return binarySearch(array, target, low, mid-1)
elif array[mid] < target:
return binarySearch(array, target, mid+1, high)
else:
return mid
arr=[1,2,3,4,5,6,7,8,9]
target=6
low=0
high=9
print(binarySearch(arr, target, low, high))C
#include<stdio.h>
int main(){
int arr[10]={1,2,3,4,5,6,7,8,9};
int target=6;
int low=0, high=9; //시작 인덱스, 끝 인덱스
int res=0;
//이분탐색 부분
while(low <= high){
int mid = (low + high) / 2;
if(arr[mid] == target)
res = mid;
if(arr[mid] > target)
high = mid - 1;
else
low = mid + 1;
}
printf("%d", res);
return 0;
}C++
#include<iostream>
using namespace std;
int main(){
int arr[10]={1,2,3,4,5,6,7,8,9};
int target=6;
int low=0, high=9; //시작 인덱스, 끝 인덱스
int res=0;
//이분탐색 부분
while(low <= high){
int mid = (low + high) / 2;
if(arr[mid] == target)
res = mid;
if(arr[mid] > target)
high = mid - 1;
else
low = mid + 1;
}
cout<<res;
return 0;
}Java
Class Main{
public static void main(){
int[] arr={1,2,3,4,5,6,7,8,9};
int start = 0;
int end = arr.length - 1;
int target=6;
int res;
while (start <= end) {
int mid = (start + end) / 2;
if (target == arr[mid])
res = mid;
else if (arr[mid] < target)
start = mid + 1;
else if (target < arr[mid])
end = mid - 1;
}
System.out.println(res);
}
}
DFS, BFS
DFS는 깊이우선탐색, BFS는 너비우선탐색이라 불리며 말 그대로 탐색하는 알고리즘이다.
DFS는 깊이우선탐색이라는 이름처럼 아래와 같이 깊이있게 탐색한다.
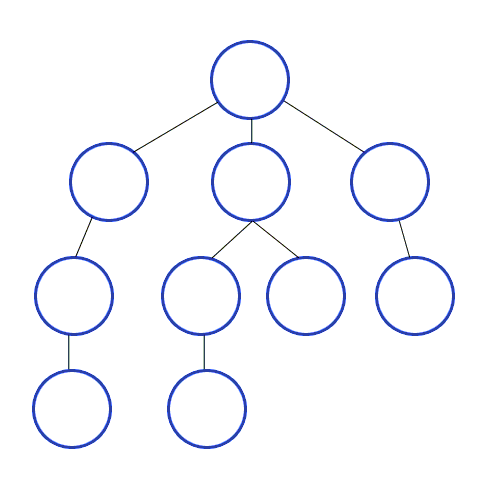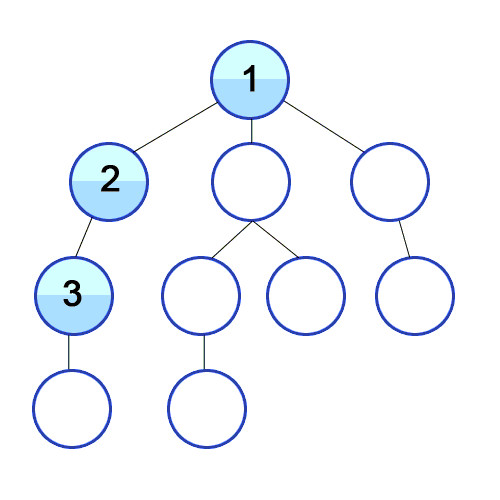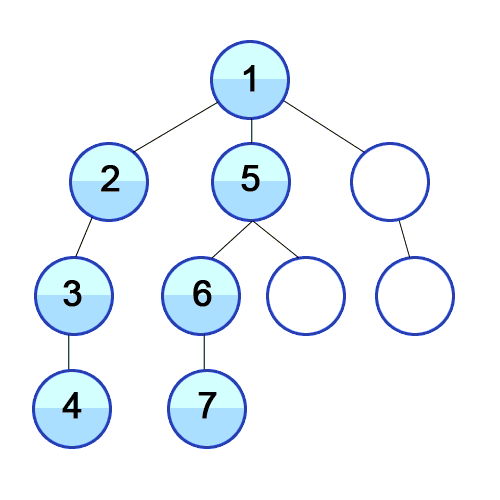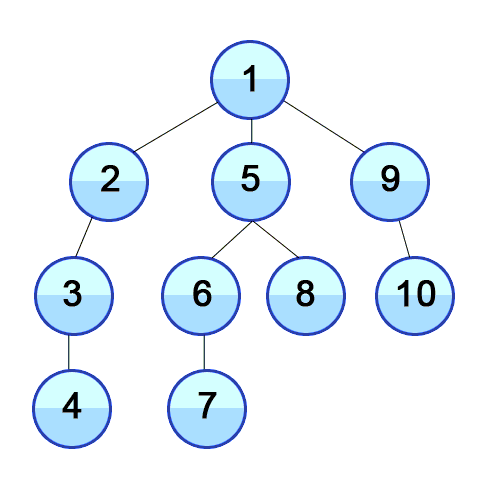
BFS는 너비우선탐색이라는 이름처럼 넓게 탐색을 한다. 회색은 큐에 들어가있는 상태이고 검은색으로 변하면 방문했다는 표시이다.
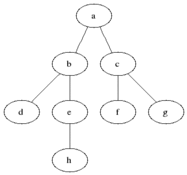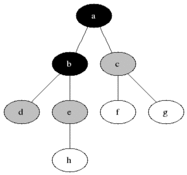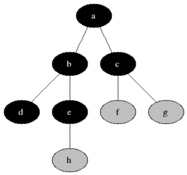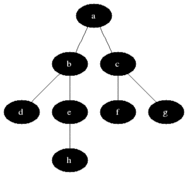
이걸 코드로 구현해보자!
Python
- 딕셔너리와 리스트를 통해 그래프를 구현할 수 있다.
DFS
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [7],
7: [6],
8: [5],
9: [1, 10],
10: [9]} //위 예시를 토대로 작성
root = 1
def DFS(graph, root):
visited = []
stack = [root]
while stack:
node = stack.pop()
print(node) //현재 방문하고 있는 노드번호 출력
if node not in visited:
visited.append(node)
stack.extend(graph[node])
return visited
print(DFS(graph, root))BFS
graph = {
'a': ['b', 'c'],
'b': ['a', 'd', 'e'],
'c': ['a', 'f', 'g'],
'd': ['b'],
'e': ['b', 'h'],
'f': ['c'],
'g': ['c']} //위 예시를 토대로 작성
root = 1
def BFS(graph, root):
visited = []
queue = []
queue.append(root)
while queue:
node = queue.pop(0)
print(node) //현재 방문하고 있는 노드번호 출력
if node not in visit:
visit.append(node)
queue.extend(graph[node])
return visit
print(BFS(graph, root))C
- 인접행렬을 사용하여 그래프를 구현한 후 탐색을 시작한다.
DFS
#include<stdio.h>
#include<string.h>
#define MAX 10
int adj[MAX][MAX];
int visited[MAX];
void DFS(int node, int N) { //정점과 정점개수
int nxt;
visited[node] = 1;
printf("%d ", node); //현재 방문하고 있는 노드번호 출력
for(int i = 1; i <= N; i++) {
if(adj[node][i]) {
nxt = i;
if(!visited[nxt])
DFS(there, N);
}
}
}
int main() {
int start, num, edge; //시작정점, 정점개수, 간선개수
int x,y;
for(int i=1; i<=edge; i++) {
scanf("%d %d", &x,&y);
adj[x][y]=1;
adj[y][x]=1; //인접행렬
//x와 y가 연결되어 있음을 저장하는 작업
}
DFS(start, num);
return 0;
}BFS
#include<stdio.h>
#include<string.h>
#define MAX 10
int adj[MAX][MAX];
int visited[MAX];
typedef struct Queue{
int front, rear;
int data[MAX];
}Queue;
void BFS(int node, int N) {
int nxt;
visited[node] = 1;
Queue q;
q.front=-1;
q.rear=-1;
q.data[++q.rear]=node;
while(q.front<q.rear){
int cur=q.data[++q.front];
printf("%d ", cur); //현재 방문하고 있는 노드번호 출력
for(int i = 1; i <= N; i++) {
if(adj[cur][i]) {
nxt = i;
if(!visited[nxt]) {
visited[nxt]=1;
q.data[++q.rear]=nxt;
}
}
}
}
}
int main() {
int start, num, edge; //시작정점, 정점개수, 간선개수
int x,y;
for(int i=1; i<=edge; i++) {
scanf("%d %d", &x,&y);
adj[x][y]=1;
adj[y][x]=1; //인접행렬
//x와 y가 연결되어 있음을 저장하는 작업
}
BFS(start, num);
return 0;
}C++
- vector을 이용하여 그래프를 구현한다.
DFS
#include<iostream>
#include<vector>
#define MAX 10
using namespace std;
bool visit[MAX]
vector<int> graph[MAX];
void dfs(int x){
visit[x]=true;
cout << x << ' '; //현재 방문하고 있는 노드번호 출력
for(int i=0;i<graph[x].size();i++){
int nxt=graph[x][i];
if(!visit[nxt])
dfs(nxt);
}
}
int main(){
int a,b;
for(int i=0;i<MAX;i++){
cin>>a>>b;
v[a].push_back(b);
v[b].push_back(a); //그래프 양방향 연결
}
dfs(1); //숫자 1인 노드가 있다고 가정하고 1부터 시작
return 0;
}BFS
#include<iostream>
#include<vector>
#include<queue>
#define MAX 10
using namespace std;
bool visit[MAX]
vector<int> graph[MAX];
void bfs(int x){
visit[x]=true;
queue<int>q;
q.push(x);
while(!q.empty()){
int cur=q.front();
q.pop();
cout << cur <<' '; //현재 방문하고 있는 노드번호 출력
for(int i=0;i<graph[cur].size();i++){
int nxt=graph[cur][i];
if(!visit[nxt]){
visit[nxt]=true;
q.push(nxt);
}
}
}
}
int main(){
int a,b;
for(int i=0;i<MAX;i++){
cin>>a>>b;
v[a].push_back(b);
v[b].push_back(a); //그래프 양방향 연결
}
bfs(1); //숫자 1인 노드가 있다고 가정하고 1부터 시작
return 0;
}Java
DFS
import java.util.ArrayList;
Class Main {
boolean[] visted = new boolean[10];
ArrayList<Integer>[] graph=new ArrayList[10]; //그래프 만들 2차원 배열
void dfs(int node) {
vistied[node] = true;
System.out.println(node);
for (int nxt : graph[node]) {
if(!vistied[nxt]) {
dfs(nxt);
}
}
}
public static void main(String[] args) {
for(int i=1;i<=9;i++){
int a = sc.nextInt();
int b = sc.nextInt();
//2차원 동적 배열에 요소 추가하기 전에 배열 추가해주기!!
if(graph[a]==null)
graph[a]=new ArrayList<Integer>();
graph[a].add(b); //a와 b노드 연결하기
graph[b].add(a);
}
dfs(1); //노드 1부터 시작한다고 가정
}
}BFS
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.Queue;
Class Main {
boolean[] visted = new boolean[10];
ArrayList<Integer>[] graph=new ArrayList[10]; //그래프 만들 2차원 배열
void bfs(int node) {
vistied[node] = true;
Queue<Integer> q=new LinkedList<Integer>();
q.add(node);
while(!q.isEmpty()){
int cur=q.poll();
System.out.println(cur);
for (int nxt : graph[cur]) {
if(!vistied[nxt]) {
visited[nxt]=true;
q.add(nxt);
}
}
}
}
public static void main(String[] args) {
for(int i=1;i<=9;i++){
int a = sc.nextInt();
int b = sc.nextInt();
//2차원 동적 배열에 요소 추가하기 전에 배열 추가해주기!!
if(graph[a]==null)
graph[a]=new ArrayList<Integer>();
graph[a].add(b); //a와 b노드 연결하기
graph[b].add(a);
}
bfs(1); //노드 1부터 시작한다고 가정
}
}'GDSC Sookmyung 활동 > Speaker Session & Hands on Workshop' 카테고리의 다른 글
| [CI/CD] CI/CD와 Github Action 살펴보기 (0) | 2022.04.03 |
|---|---|
| [Web Session] http 웹 기본 지식 (0) | 2021.12.27 |
| [Git/GitHub Session] Git 시작하기 (0) | 2021.09.27 |
| [Clean Code] 가독성 좋은 코드 작성 팁 (0) | 2021.05.03 |
| [Git/GitHub Session] Git, GitHub 시작하기 (0) | 2021.03.27 |
