목차
더보기
1. Sigmoid 함수의 문제점
2. Relu 함수
3. Weight Initialization
4. Dropout
5. Batch Norm
6. ConvNet
1. Sigmoid 함수의 문제점
기존 Neural Network의 학습 과정
- 기존 neural network는 어떠한 입력을 받고 그에 해당하는 결과를 출력한다.

- 이때 그 결과와 실제 데이터(ground truth data)의 차이를 로스라고 한다.
- 로스값을 미분한 것을 Gradient라고 하고 그래프의 관점에서 기울기에 해당한다.
- Gradient를 Back propagation하면서 네트워크를 학습시킨다.
- Sigmoid 함수 그래프를 보면 0 주변의 기울기 값이 매우 크다는 것을 알 수 있다.

- 반면 극단 좌표계 쪽의 기울기 값은 매우 작다.

- 그렇다면 Gradient를 전달받아서 Neural network가 학습할 때 매우 작은 값을 받을 수 있고 그 확률이 굉장히 높다.
- 만약 네트워크가 깊다면 Sigmoid 함수 개수가 늘어나면서 매우 작은 값을 가진 Gradient가 곱해지고 결국 소실된다. 이를 vanishing gradient라고 한다.

- 따라서 Gradient가 사라지면서 네트워크 학습이 안되는 vanishing gradient가 Sigmoid 함수의 문제점이다.

2. Relu 함수
Relu함수란?
- x값을 받았을 때 양수라면 x를 그대로 반환하고 음수라면 0을 반환한다.

Relu 함수의 Gradient 알아보기
- Relu를 그래프로 나타냈을 때 입력값이 양수라면 그대로 반환하기 때문에 y=x이므로 기울기가 1이다.

- 따라서 아무리 네트워크가 깊더라도 Gradient가 잘 전달될 수 있다.
- 반면 입력값이 음수라면 0을 반환하므로 아예 전달이 안되는 문제점이 있다.

3. Weight Initialization
Xavier(Glorot) Initialization이란?
- 다음은 네트워크가 어떻게 학습이 되어가는지 보여주는 그래프이다.

- 네트워크 학습의 목표는 로스가 가장 최저인(기울기가 0인) 지점을 찾는 것이다.
- 실제 로스 그래프는 굉장히 복잡한 형태를 가진다.

- A지점에서 출발했을 때 로스의 최소가 아닌 곳으로 학습을 진행한다면 Global Minima가 아닌 Local Minima에 도달하거나 Saddle point에 빠질 위험이 있다.
- 반면 Global Minima에 가까운 위치에서 출발한다면 쉽게 수렴할 수 있다.

- 즉, 어디서 출발할 것인지에 따라 결과값이 달라지므로 그 지점을 설정하는 것을 Xavier(Glorot) Initialization라고 한다.
- 기존에 weight을 초기화할 땐 random Initialization을 사용했다. 즉, 평균은 0, 분산은 1으로 설정했다.
- Xavier은 평균은 0, 분산은 다음과 같이 구성된다.

- Channel_in은 입력의 채널 개수, Channel_out은 출력의 채널 개수이다.
He Initialization for Relu이란?
- Relu 함수에 특화된 weight 초기화 방식이다.
- 평균은 0, 분산은 Xavier의 2배 크게 설정한다.

4. Dropout
Dropout의 필요성
- 다음은 데이터셋 샘플의 분포이다. 그리고 핑크선은 네트워크가 학습 데이터셋을 Regression하는 선이다.

- 첫번째 경우 학습 데이터셋을 3개, 두번째는 6개, 세번째는 다 맞춘것을 확인할 수 있다. 이를 각각 under-fitting, over-fitting이라고 한다.
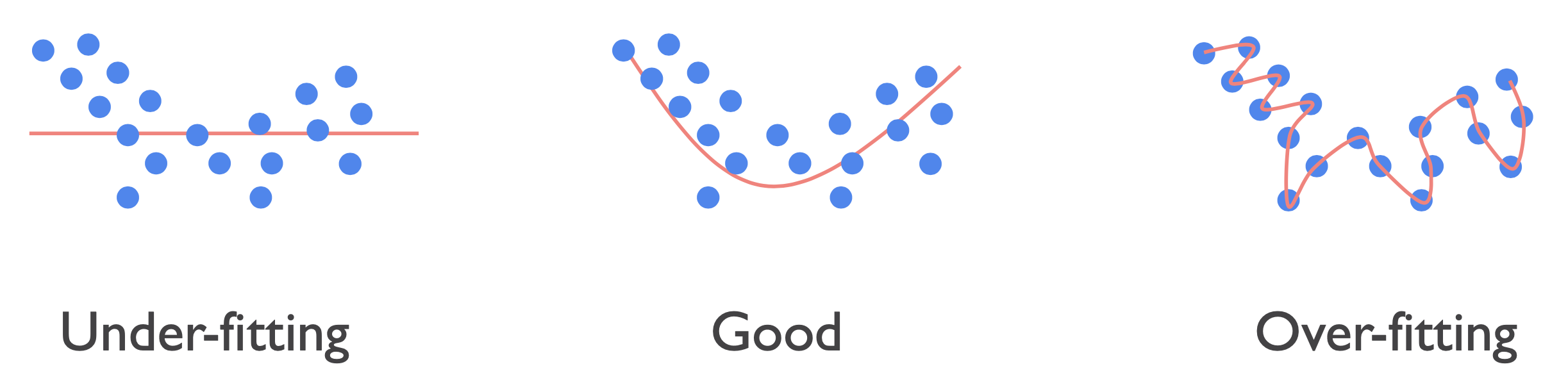
- 즉 under-fitting의 경우 학습 데이터셋에 대한 정확도가 매우 낮고 over-fitting은 매우 높은 것을 의미한다.
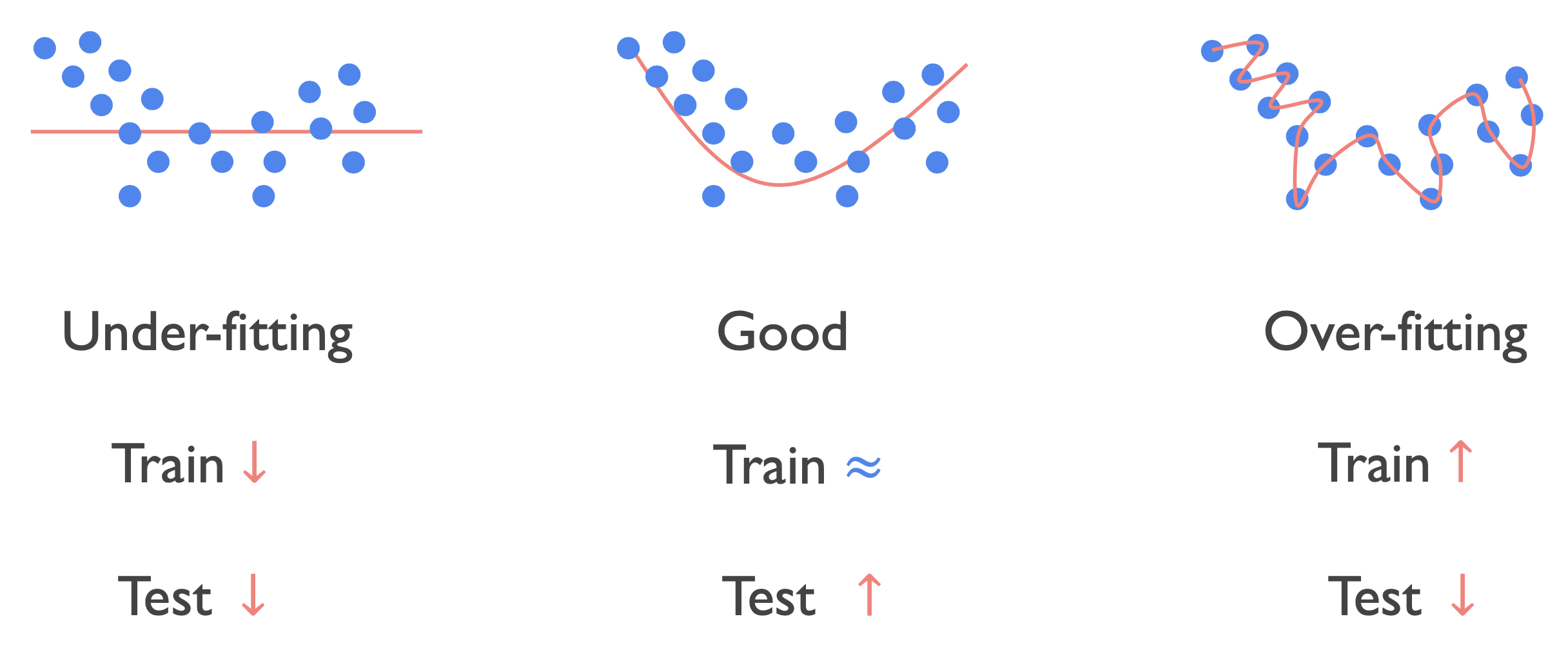
- under-fitting의 경우 정확도를 높이도록 쉽게 컨셉을 잡을 수 있다. 하지만 over-fitting의 경우 학습 데이터셋의 정확도는 높은데 테스트 데이터셋의 정확도는 낮은지 원인을 파악하기 쉽지 않다.
- over-fitting은 학습 데이터셋에 과도하게 맞춰져서 테스트 데이터셋은 아예 못맞추는 오류를 말한다.
- 가운데의 분포와 같이 학습 데이터셋의 정확도가 적절히 피팅됐기 때문에 실제 테스트 데이터셋에서 정확도가 높은 것을 알 수 있다.
Dropout이란?
- 네트워크의 목표는 over-fitting을 막고 under-fitting을 피해 가운데와 같은 양상을 띄는 것이다.
- 이때의 가장 최적의 피팅을 만드는 것을 도와주는 Ragularation이다.
- 다음은 입력이 고양이인지 아닌지를 맞추는 네트워크이다.

- 전체 노드를 거치는 것을 방지하기 위해 특정 일부분의 노드를 꺼서 학습하는 것을 Dropout이라고 한다.
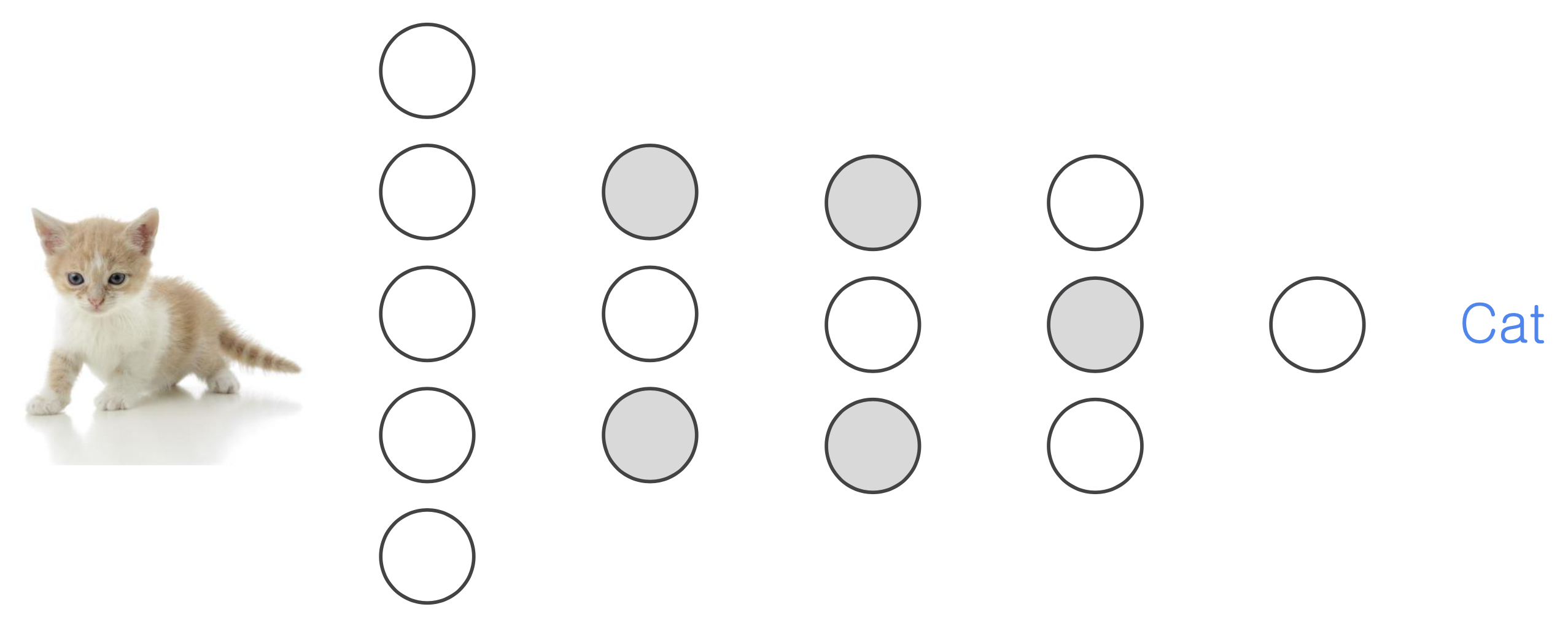
- 즉, 모든 노드(뉴런)을 사용하는 것이 아니라 일부분에 대해서만 학습하는 것이다.
- 이때 노드를 끄는 것은 랜덤하게 설정된다.
- 고양이의 전체를 학습하지 않고 특정 부분, 예를 들어 귀, 꼬리, 발톱을 가지고 학습하기 때문에 테스트 데이터에서 새로운 종류의 고양이들도 고양이라고 맞출 수 있다.
5. Batch Norm
Batch Normalization이란?
- 다음은 입력이 고양이인지 아닌지를 맞추는 네트워크이다.

- 이때 입력 데이터의 분포를 살펴보자.

- 이미지의 분포가 이상적인 곡선으로 형성된다면 네트워크를 지나면서 형태가 점점 망가진다. 이를 Internal Covariate Shift라고 한다.
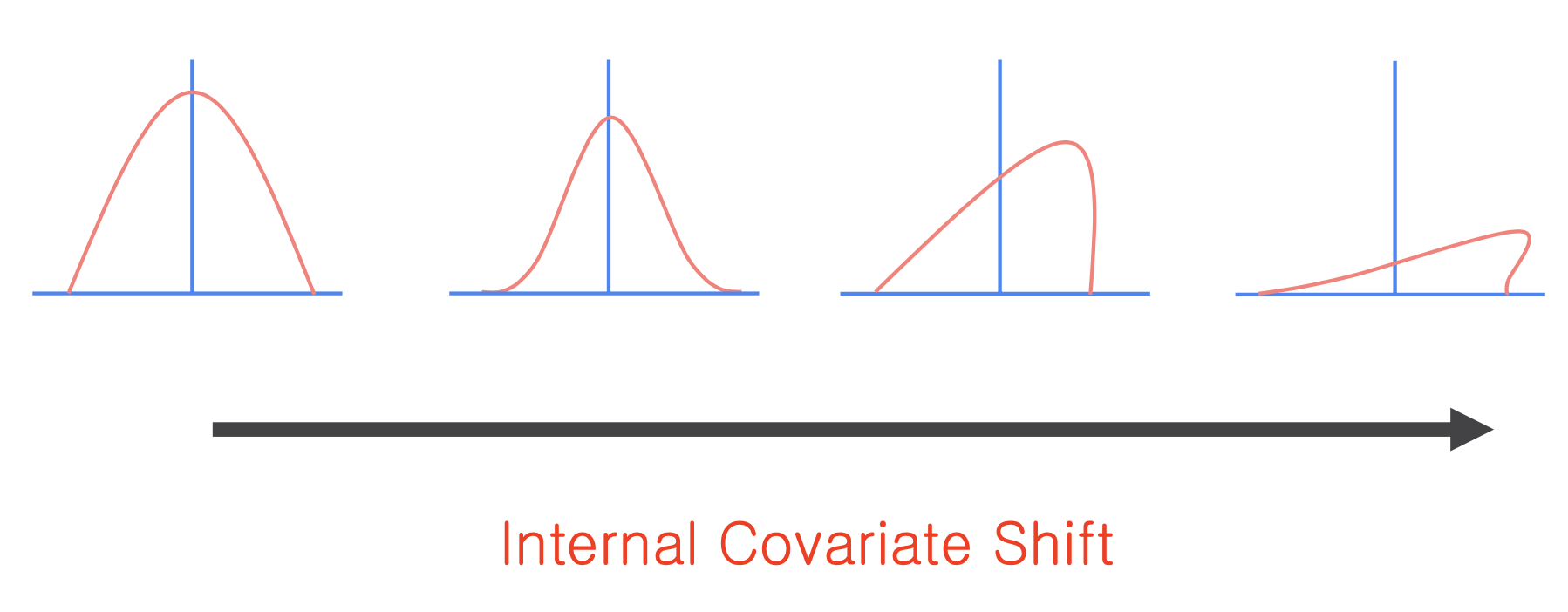
- Batch Normalization은 Internal Covariate Shift를 막기 위해 첫번째 입력으로 들어온 분포를 Normalization을 해서 항상 일정하게 유지시킨다.

6. ConvNet
ConvNet의 Conv 레이어 만들기
- 32*32*3 크기의 이미지를 입력값으로 하자.
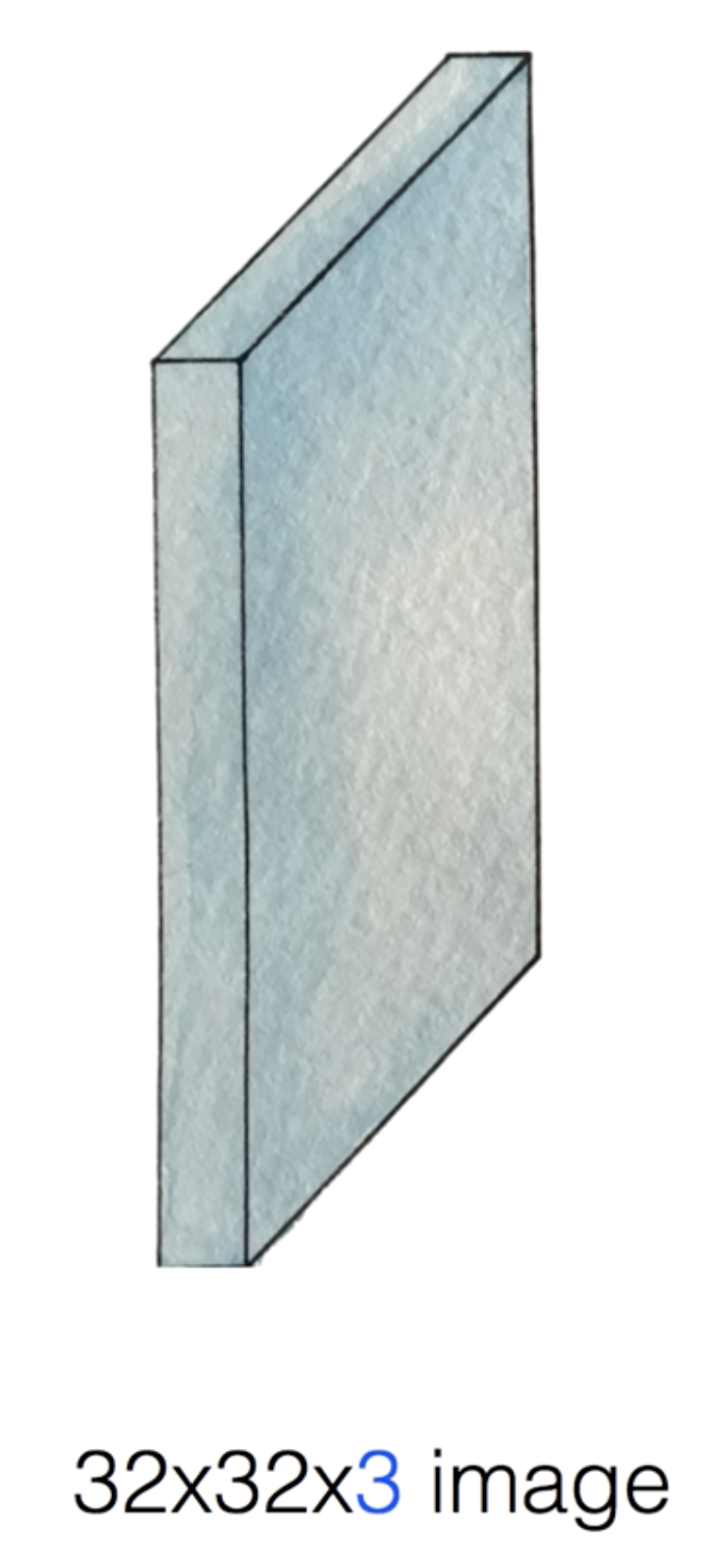
- 3은 컬러 사진임으로 RGB를 뜻한다.
- 전체 이미지를 하나의 입력으로 받지 않고 필터만큼 일부분씩 처리한다. 필터의 크기는 원하는 대로 설정한다.
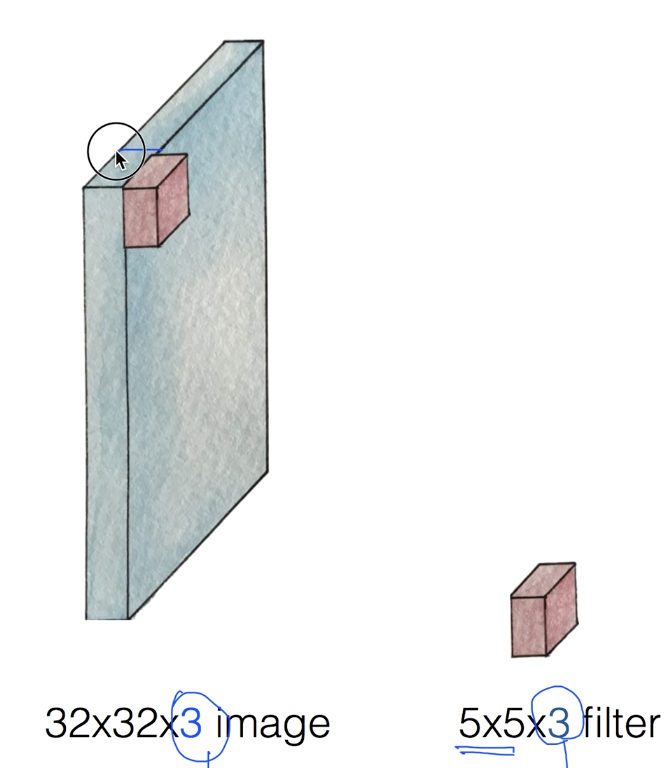
- 필터에 의해 32*32 중 5*5 만큼만 읽어들이고 처리 후 한 숫자만 뽑아낸다.

- Regression과 같이 Wx+b를 활용해서 한 숫자를 뽑아낼 수 있다. ReLu 함수를 사용한다.
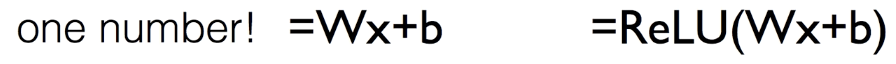
- 필터가 n칸씩(stride) 이동하면서 전체 이미지를 읽는다면 (n-f)/stride+1개의 숫자를 뽑아낸다.
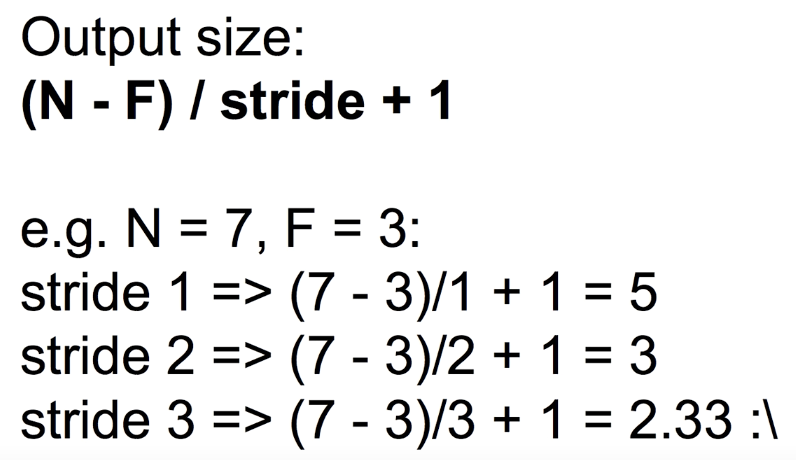
- stride가 커질수록 이미지가 작아지기 때문에 모서리에 padding으로 감싸 손실 정보를 제거한다.

- 즉, n*n 이미지가 padding에 감싸져 있다면 ConvNet에서 필터에 의해 크기가 줄어들지 않고 그대로 유지된다.
- 이미지 입력에 대해 6개의 필터를 적용하자.

- 각각의 필터는 weight이 다르기 때문에 결과값은 다르게 나온다.
- 6개의 필터를 ConvNet에 적용시키면 깊이가 6이 된다는 것을 알 수 있다.
- 여러개의 ConvNet을 적용시킬 수 있다. 하지만 각 상황 별 필터의 깊이에 주의해야 한다.
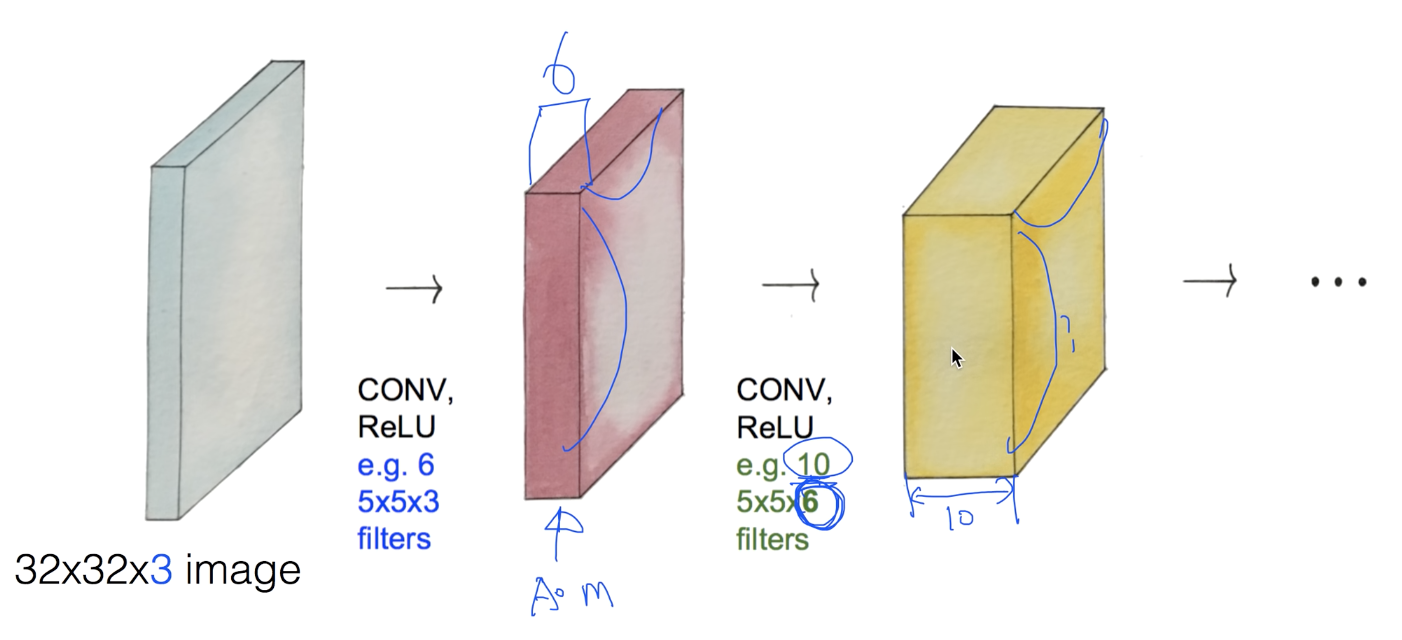
- weight 변수는 필터의 크기*개수이고 초기화 이후 학습에 사용되면서 업데이트 된다.
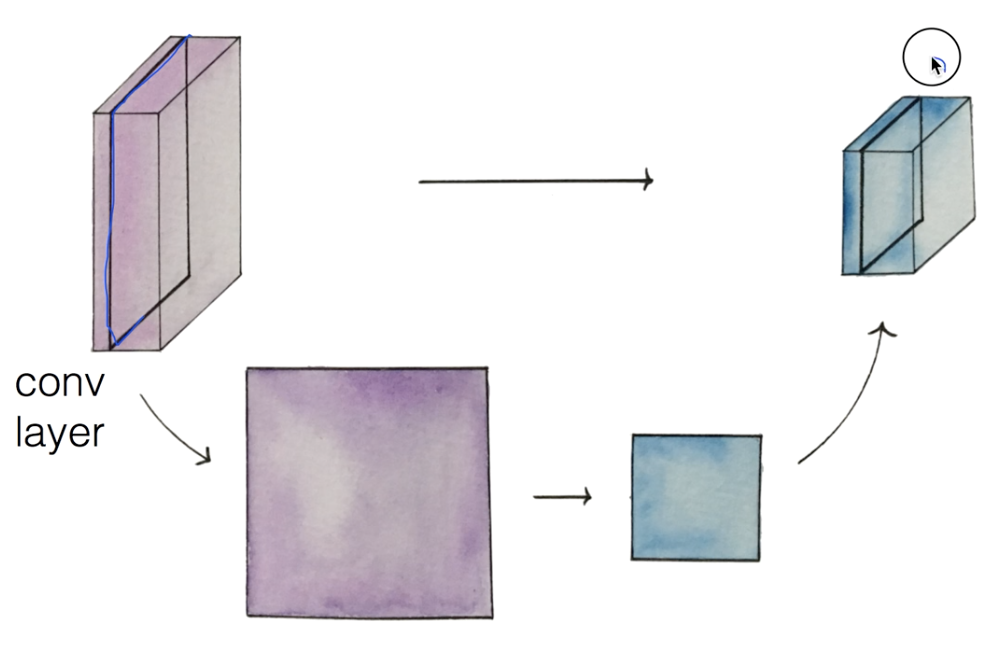
Max pooling과 Full Network
- 입력 이미지를 ConvNet을 적용시켜 필터만큼 두꺼워진다. 이것의 한 레이어를 작은 사이즈로 축소시켜서 합치는 것을 Pooling Layer라고 한다.
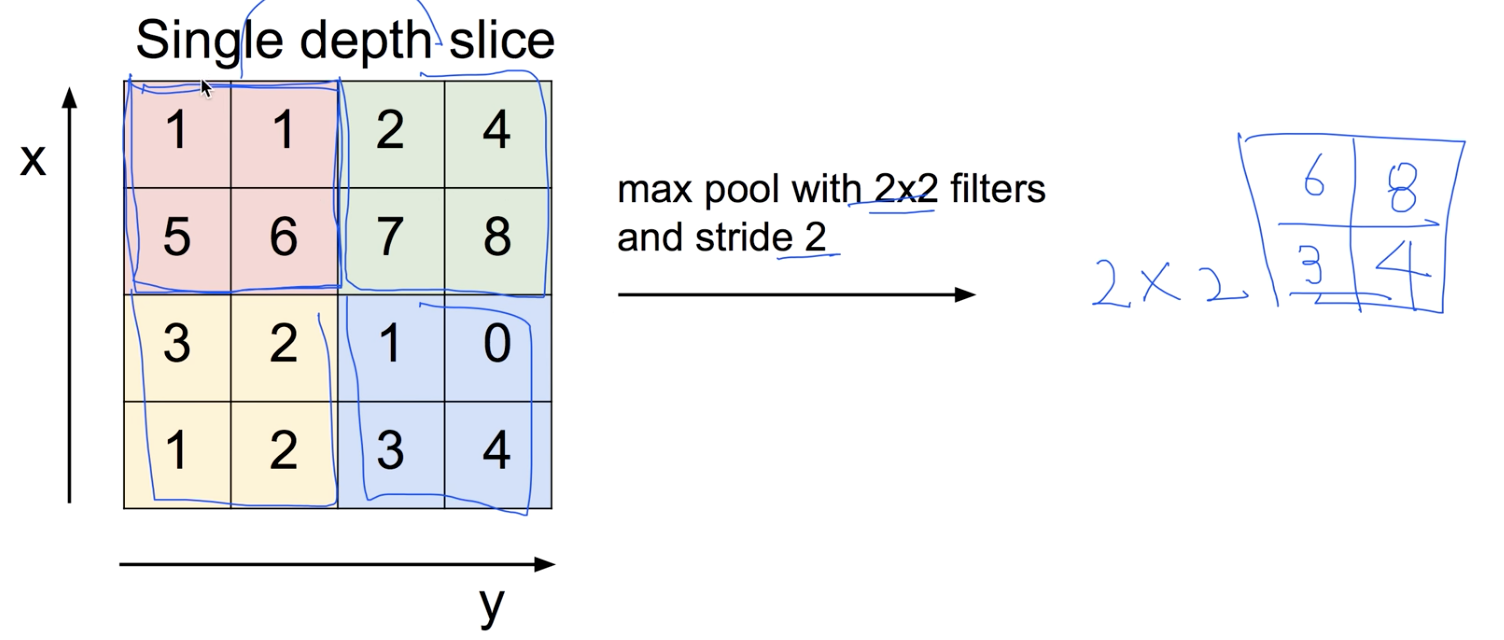
- 한 필터에서 가장 큰 값을 뽑아서 사이즈를 축소시키는 Pooling 방법을 Max Pooling이라고 한다.
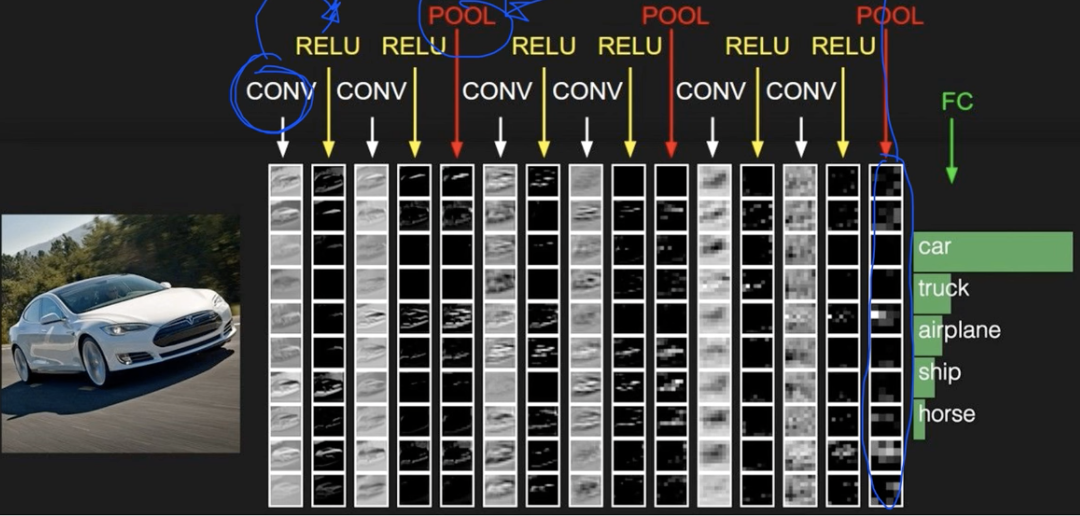
- Fully Connected Layer를 ConvNet, Relu, Pooling 레이어를 원하는 순서대로 쌓고 마지막에 Pooling으로 구성한다.
'Group Study (2022-2023) > Machine Learning' 카테고리의 다른 글
| Part 3. Convolutional Neural Network(2) (0) | 2022.11.26 |
|---|---|
| [Machine Learning] 7주차 스터디 - PART 3: Convolutional Neural Network (2) / Side Project Team Building (0) | 2022.11.21 |
| [Machine Learning] 5주차 스터디 - PART 2: Basic Deep Learning (0) | 2022.11.18 |
| [Machine Learning] 6주차 스터디 - Object Detection: YOLOv1~v2 (0) | 2022.11.15 |
| [Machine Learning] 5주차 스터디 - Object Detection: -stage-detector (0) | 2022.11.13 |