비지도 학습이란?
정답(target, label)이 없고 특성 데이터만 주어지는 학습 방법이다.
종류는 군집과 차원 축소로 나눌 수 있다.
1. 군집 알고리즘
군집 (클러스터) : 비슷한 패턴들을 묶어놓은 집단
1) 데이터 준비
가로 100px, 세로 100px의 사과, 파인애플, 바나나 사진을 각 100개씩 준비하여 numpy 배열로 변환한다.
# !: shell 명령어
!wget https://bit.ly/fruits_300_data -O fruits_300.npy
import numpy as np
import matplotlib.pyplot as plt
fruits = np.load('fruits_300.npy')
print(fruits.shape)
# (300, 100, 100) <- 100 x 100 픽셀의 300개 샘플
2) 분석
Matlplotlib의 imshow()를 통해 넘파이 배열로 저장된 값을 이미지로 출력할 수 있다.
이때 픽셀 값이 크면 흰색(255)에 가깝고, 작으면 검은색(0)에 가깝다. (중간에 큰 숫자들은 사과의 꼭지 부분)
plt.imshow(fruits[0], cmap='gray') # cmap: 색
plt.show()
print(fruits[0, 0, :]) # 1행의 전체 1열 출력
# [ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1
# 2 2 2 2 2 2 1 1 1 1 1 1 1 1 2 3 2 1
# 2 1 1 1 1 2 1 3 2 1 3 1 4 1 2 5 5 5
# 19 148 192 117 28 1 1 2 1 4 1 1 3 1 1 1 1 1
# 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
# 1 1 1 1 1 1 1 1 1 1]
fig, axs = plt.subplots(1, 2)
axs[0].imshow(fruits[100], cmap='gray_r') # 색 반전
axs[1].imshow(fruits[200], cmap='gray_r')
plt.show()
이제, 샘플의 차원을 변경하여 평균을 가지고 다양하게 분석해보자.
apple = fruits[0:100].reshape(-1, 100*100) # 100 x 100 -> 10000
pineapple = fruits[100:200].reshape(-1, 100*100)
banana = fruits[200:300].reshape(-1, 100*100)# 샘플 평균의 히스토그램
# axis=1 : 열 방향으로 계산하여 샘플 100개의 평균 반환
plt.hist(np.mean(apple, axis=1), alpha=0.8)
plt.hist(np.mean(pineapple, axis=1), alpha=0.8)
plt.hist(np.mean(banana, axis=1), alpha=0.8)
plt.legend(['apple', 'pineapple', 'banana'])
plt.show()
샘플 평균으로는 사과와 파인애플을 구별하기 어렵다. 이번에는 픽셀 평균으로 히스토그램을 그려보자.
# 픽셀 평균의 히스토그램
# 여러 그래프를 한 이미지에 (1: 행, 3: 열)
fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].bar(range(10000), np.mean(apple, axis=0))
axs[1].bar(range(10000), np.mean(pineapple, axis=0))
axs[2].bar(range(10000), np.mean(banana, axis=0))
plt.show()
픽셀 값이 크면 밝은 색이고, 작으면 어두운 색이다. 100x100 크기로 평균을 만든 뒤 위에서처럼 이미지로 표현해보자.
apple_mean = np.mean(apple, axis=0).reshape(100, 100)
pineapple_mean = np.mean(pineapple, axis=0).reshape(100, 100)
banana_mean = np.mean(banana, axis=0).reshape(100, 100)
# 각 과일의 평균 이미지
fig, axs = plt.subplots(1, 3, figsize=(20, 5))
axs[0].imshow(apple_mean, cmap='gray_r')
axs[1].imshow(pineapple_mean, cmap='gray_r')
axs[2].imshow(banana_mean, cmap='gray_r')
plt.show()
3) 군집 (Clustering)
특정 과일의 평균값과 가까운 사진들을 골라 군집화해보자.
# 300개 샘플의 픽셀 100x100개 평균
abs_diff = np.abs(fruits - apple_mean)
abs_mean = np.mean(abs_diff, axis=(1,2))
apple_index = np.argsort(abs_mean)[:100] # 평균이 가장 작은 값 100개
fig, axs = plt.subplots(10, 10, figsize=(10,10)) # 10x10 이미지
for i in range(10):
for j in range(10):
axs[i, j].imshow(fruits[apple_index[i*10 + j]], cmap='gray_r')
axs[i, j].axis('off')
plt.show()
2. K - 평균
* 클러스터의 중심 = 센트로이드
k(센트로이드 및 군집 개수)를 미리 정하고 클러스터로 묶음 (첫 센트로이드들은 랜덤으로 잡아줌)
-> 중심을 다시 계산해서 바뀐 중심을 토대로 군집화 (이때, 개수가 많은 쪽으로 중심이 이동함)
-> 중심이 바뀌지 않을 때까지 반복

fruits_2d = fruits.reshape(-1, 100*100) # 3차원 -> 2차원 배열
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42) # n_iter: 반복 횟수 (기본 10)
km.fit(fruits_2d)
print(np.unique(km.labels_, return_counts=True)) # 비슷한 비율
# (array([0, 1, 2], dtype=int32), array([111, 98, 91]))KMeans 클래스를 통해 n_clusters로 k를 정하고, fit()으로 비지도 학습을 진행한다. 그 결과, 데이터들은 비슷한 비율만큼 0/1/2로 라벨링되었다.
import matplotlib.pyplot as plt
def draw_fruits(arr, ratio=1):
n = len(arr) # n은 샘플 개수입니다
# 한 줄에 10개씩 이미지를 그립니다. 샘플 개수를 10으로 나누어 전체 행 개수를 계산합니다.
rows = int(np.ceil(n/10))
# 행이 1개 이면 열 개수는 샘플 개수입니다. 그렇지 않으면 10개입니다.
cols = n if rows < 2 else 10
fig, axs = plt.subplots(rows, cols,
figsize=(cols*ratio, rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n: # n 개까지만 그립니다.
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i, j].axis('off')
plt.show()


draw_fruits()를 만들어 각 라벨이 0/1/2인 경우, 군집화된 이미지들을 그려보았다. 거의 정답과 유사하게 묶였지만, 파인애플을 묶는 과정에서 사과와 바나나가 조금 섞인 것을 볼 수 있다.
print(km.transform(fruits_2d[100:101])) # 센트로이드 간 거리로 특성 축소
# [[3393.8136117 8837.37750892 5267.70439881]]
print(km.predict(fruits_2d[100:101])) # 가장 작은 값이 가장 가까움
# [0]
draw_fruits(fruits[100:101]) # 파인애플!
print(km.n_iter_) # 수렴까지 반복 횟수
# 4transform()으로 10,000개의 특성을 3개의 특성(각 센트로이드 간 거리)으로 축소해봤다. 이후 predict()로 어떤 센트로이드와 가장 가까운지, 그래서 어떤 클러스터로 묶이는지 볼 수 있다. 실제로 이미지를 출력해보면 파인애플이 나오는 것을 확인할 수 있다.
이때 드는 의문, 어떤 k가 가장 적합할까? 최적의 k를 찾으려면 직접 구해보는 수밖에 없다. 엘보우 메소드를 이용해서 알아보자.
엘보우 메소드: 중심 주변 샘플들의 중심까지의 거리 평균을 구하면, k값이 늘어도 inertia가 그다지 줄지 않는 지점이 최적의 값이어서 꺾인 그래프가 그려진다.
* inertia: 클러스터 중심과 샘플 사이 거리의 제곱 합 (센트로이드와 모여있는 정도)
⇒ 클러스터 개수가 늘어나면, 각 클러스터의 크기가 줄어들어 intertia도 줄음!
inertia = []
for k in range(2, 7):
km = KMeans(n_clusters=k, n_init='auto', random_state=42)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2, 7), inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()
따라서, k가 3일 때 가장 적합하다.
3. 주성분 분석
"특성의 개수 줄이기"
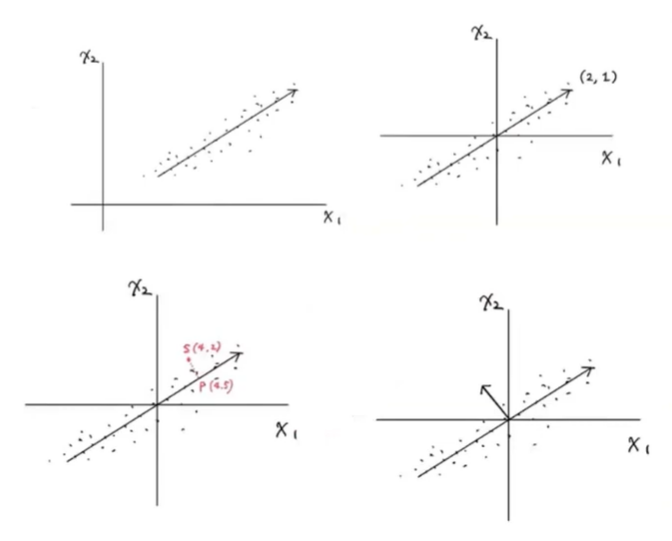
산점도를 그렸을 때, 한쪽으로 가장 많이 퍼져 있는 방향을 찾아 주성분을 뽑아낼 수 있다. (사이킷런은 원점에 맞춰줌)
=> 두 개의 특성을 하나의 data point(벡터의 원소)로 변환 가능 (정방향 or 수직 방향)
from sklearn.decomposition import PCA
pca = PCA(n_components=50) # n_components: 주성분 개수
pca.fit(fruits_2d)
print(pca.components_.shape) # 50개 주성분, 10000개의 특성
# (50, 10000)
draw_fruits(pca.components_.reshape(-1, 100, 100))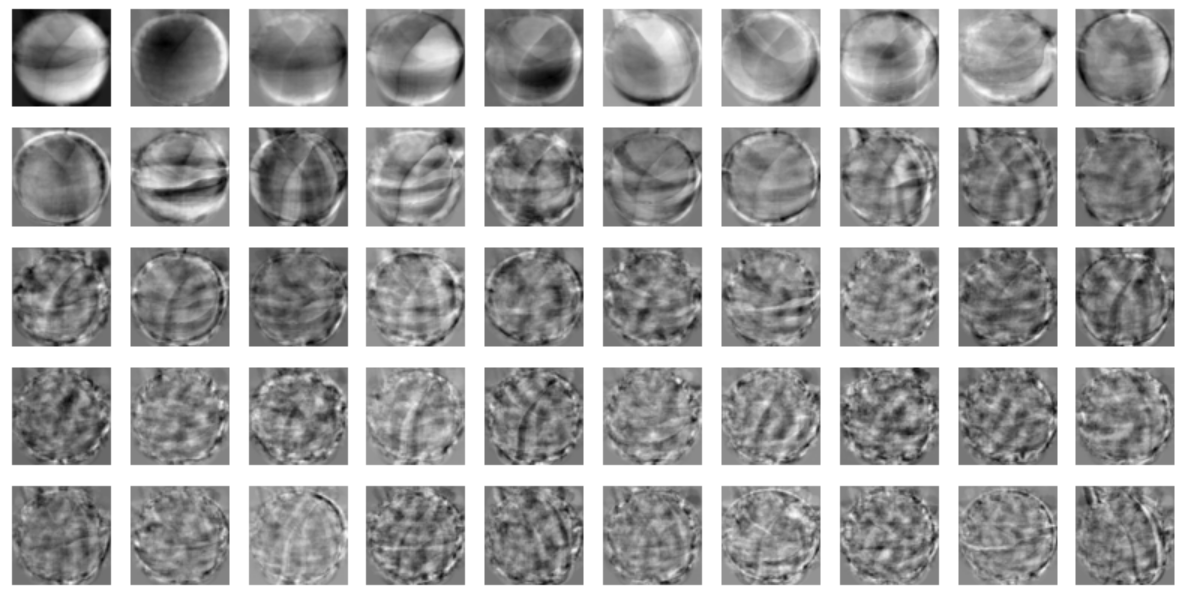
PCA 클래스를 이용하면, 원본 데이터를 많이 반영하는 주성분들을 찾을 수 있다.
print(fruits_2d.shape) # 원본 데이터
# (300, 10000)
fruits_pca = pca.transform(fruits_2d) # 주성분으로 변환
print(fruits_pca.shape)
# (300, 50)
# 주성분 가지고 원본 특성 복원
fruits_inverse = pca.inverse_transform(fruits_pca)
print(fruits_inverse.shape)
# (300, 10000)
fruits_reconstruct = fruits_inverse.reshape(-1, 100, 100)
for start in [0, 100, 200]:
draw_fruits(fruits_reconstruct[start:start+100])
print("\n")


transform()으로 원본 데이터에서 주성분으로 변환할 수 있다. 이와 반대로, inverse_transform()을 이용하면 비록 완벽하진 않지만, 주성분에서 원본 특성을 복원할 수 있다.
# explained_variance_ratio: 50개 주성분의 분산 비율
print(np.sum(pca.explained_variance_ratio_))
# 0.9214971223073142
plt.plot(pca.explained_variance_ratio_)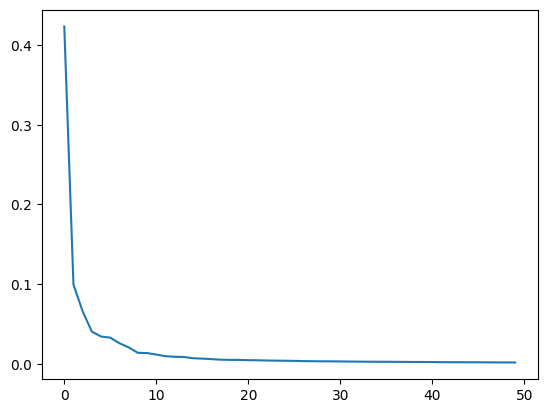
50개의 주성분들이 분산을 얼만큼 나타내는지 explained_variance_ratio로 확인할 수 있다. PCA는 분산이 최대인 축을 찾는 과정이기 때문에, 주성분은 큰 분산 비율을 가지고 있다. 그래프를 보면, 10개 이상부터의 주성분들은 큰 역할을 하지 않는다는 것을 알 수 있다.
또한, 주성분들은 다른 알고리즘(ex. Logistic Regression, 군집 등)과 함께 사용될 수 있기 때문에 유용하다. 기존처럼 원본 데이터를 다 주는 대신에 주성분을 줌으로써, 적은 데이터의 양으로 유사한 결과를 얻을 수 있다.
⭐ 요약
1. 비지도 학습은 타깃 없이 특성들만 가지고 학습하며, 군집과 차원 축소로 나뉜다.
2. k - 평균은 랜덤으로 받은 센트로이드들을 중심으로 샘플을 묶고, 중심이 이동하지 않을 때까지 중심을 다시 계산하여 군집화하는 것을 반복한다.
3. k - 평균에서 최적의 클러스터 개수(k)를 찾는 방식으로 엘보우 메소드가 있다.
4. 주성분 분석을 통해 특성(차원)을 축소하여 디스크 용량을 줄일 수 있다.
* 참고자료: 혼자 공부하는 머신러닝+딥러닝 (박해선)
'Group Study (2023-2024) > Machine Learning 입문' 카테고리의 다른 글
| [ML입문] week6 - 순환 신경망 (1) | 2023.12.11 |
|---|---|
| [ML입문] week5 - 딥러닝 (0) | 2023.12.04 |
| [ML입문] week3 - 분류 알고리즘(2), 트리 알고리즘 (0) | 2023.11.21 |
| [ML입문] week2 - 회귀 알고리즘과 모델 규제, 분류 알고리즘(1) (1) | 2023.11.13 |
| [ML입문] week1 - 나의 첫 머신러닝, 데이터 다루기 (1) | 2023.11.06 |