1. K - 최근접 이웃 회귀
회귀 (Regression) : 임의의 숫자(target)를 예측하는 것
=> 타깃을 따로 만들 필요 없이, 훈련 데이터의 특성 중 하나가 타깃값이 된다

[문제] 농어의 길이와 무게를 학습하여, 농어의 길이를 통해 무게를 예측해보자.
1) 데이터 준비
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)K - 최근접 이웃 분류 때와 마찬가지로 사이킷런의 train_test_split을 이용해 훈련 세트와 테스트 세트를 나눈다.
이때, 회귀는 임의의 숫자가 타깃이기 때문에 랜덤하게 섞어주면 된다. (stratify를 잘 사용하지 않음)
2) K - 최근접 이웃 회귀 사용
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
knr.fit(train_input, train_target) # k-최근접 이웃 회귀 모델 훈련
knr.score(test_input, test_target) # 결정 계수 반환score()는 결정 계수(R^2)를 반환한다.

- R^2 = 0 (타깃 = 평균, 분자가 1) → 좋지 않은 모델
- R^2 = 1 (타깃 = 예측, 분자가 0) → 좋은 모델
따라서, score()의 값이 1에 가까울 수록 좋은 모델이다.
print(knr.predict([[50]])) # 무게 예측predict()로 농어의 예측 무게(Y, 타깃)를 얻을 수 있다.
3) 과대적합 & 과소적합
- 과대적합 (Overfitting) : 훈련 세트에 지나치게 최적화된 상태 (훈련 세트 점수 >> 테스트 세트 점수)
-> 이웃 개수가 적을 때 생긴다. (if 이웃 = 1 -> 예측값이 들쑥날쑥)
- 과소적합 (Underfitting) : 모델이 충분히 복잡하지 않아 훈련 세트의 패턴을 잘 반영하지 못함 (훈련 세트 점수 < 테스트 세트 점수)
-> 이웃 개수가 많을 때 생긴다. (if 이웃 = 전체 훈련 개수 -> 무조건 하나의 값으로 예측)
따라서, 훈련/테스트의 결정 계수(R2)가 모두 어느 정도 크고, 테스트 세트보다 훈련 세트의 점수가 높아야 한다.
knr.n_neighbors = 3 # 이웃 개수(하이퍼 파라미터) 설정K - 최근접 이웃 회귀에서는 n_neighbors로 과대적합/과소적합을 조절할 수 있다.
2. 선형 회귀
1) 선형 회귀 (Linear Regression)
훈련 데이터를 반영하는 직선의 방정식을 통해 특정 숫자값 예측
=> y = a(기울기)x + b(절편)
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_input, train_target) # 선형 회귀 모델 훈련
print(lr.predict([[50]])) # 50cm 농어에 대한 예측 (ex. [1241.83860323])
print(lr.coef_, lr.intercept_) # coef_: 기울기, intercept_: 절편# 훈련 세트의 산점도
plt.scatter(train_input, train_target)
# 15에서 50까지의 1차 방정식 그래프
plt.plot([15, 50], [15*lr.coef_+lr.intercept_, 50*lr.coef_+lr.intercept_])
plt.scatter(50, 1241.8, marker='^') # 50cm 농어 데이터
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
2) 다항 회귀 (Polynomial Regression)
훈련 데이터를 반영하는 방정식이 2차 이상인 경우
예시) 2차 방정식
train_poly = np.column_stack((train_input ** 2, train_input)) # 열 방향으로 붙임
test_poly = np.column_stack((test_input ** 2, test_input))넘파이의 column_stack()을 이용해 기존 데이터에 train_input의 거듭제곱을 추가한다.
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.predict([[50**2, 50]])) # 50cm 농어의 무게 예측
print(lr.coef_, lr.intercept_) # y = ax^2 + bx + c (기울기 = a, b / 절편 = c)
# [1.01433211 -21.55792498] 116.0502107827827# 구간별 직선을 그리기 위해 15에서 49까지 정수 배열 생성
point = np.arange(15, 50)
# 훈련 세트의 산점도
plt.scatter(train_input, train_target)
# 15에서 49까지의 2차 방정식 그래프
plt.plot(point, 1.01*point**2 - 21.6*point + 116.05)
plt.scatter([50], [1574], marker='^') # 50cm 농어 데이터
plt.xlabel('length')
plt.ylabel('weight')
plt.show()
3. 특성 공학
특성 공학 (Feature Engineering) : 특성을 추가하거나 조합하는 등의 동작 수행
다중 회귀 (Multiple/Multinomial Regression) : 특성이 여러 개인 회귀 분석
[문제] 농어의 길이, 높이, 무게를 학습하여 농어의 무게를 예측해보자.
1) 특성 전처리
from sklearn.preprocessing import PolynomialFeatures # 변환기: 특성 전처리 (ex. PolynomialFeatures)
# 매개변수 degree (기본값 2 -> 거듭제곱)
poly = PolynomialFeatures(include_bias=False) # 절편 위한 1을 뺌
poly.fit(train_input)
train_poly = poly.transform(train_input)
poly.get_feature_names_out() # x0: 길이, x1: 높이, x2: 무게
# array(['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2', 'x2^2'], dtype=object)
test_poly = poly.transform(test_input) # 테스트 세트도 변환
2) 다중 회귀
선형 회귀에 똑같이 넣고 수행하면 된다.
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(train_poly, train_target)
print(lr.score(train_poly, train_target))
# 0.9903183436982125
print(lr.score(test_poly, test_target))
# 0.9714559911594111만약 degree를 증가시켜서 특성을 늘리면, 너무 복잡한 모델이 되어 과대적합이 발생한다.
poly = PolynomialFeatures(degree=5, include_bias=False)
# ...
# 특성 전처리 후 선형 회귀 똑같이 학습
# ...
print(lr.score(test_poly, test_target)) # 과대적합 (하나도 못 맞힘)
# -144.405794368449484. 규제
가중치(기울기)를 작게 하여 과대적합 완화
1) 표준화
from sklearn.preprocessing import StandardScaler
ss = StandardScaler() # 표준점수
ss.fit(train_poly) # 각 특성의 표준점수 구함
train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)특성 스케일이 비슷해야 기울기에 적용되는 규제도 공평해진다.
2) 릿지 (Ridge)
가중치^2로 규제 (=L2 규제)
-> 선형 회귀에서 L2 규제가 적용된 것을 릿지라고 부름
최적의 alpha(규제 강도)를 찾는 것이 중요하다. (직접 그래프를 그려보지 않으면 모름)
import matplotlib.pyplot as plt
train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100] # 매개변수 alpha의 기본값 = 1
for alpha in alpha_list:
ridge = Ridge(alpha=alpha) # 릿지 모델 생성
ridge.fit(train_scaled, train_target) # 릿지 모델 훈련
train_score.append(ridge.score(train_scaled, train_target))
test_score.append(ridge.score(test_scaled, test_target))
plt.plot(np.log10(alpha_list), train_score) # log10으로 변환하는 게 관습 (알파값 간격 맞추려고)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show() # 규제를 많이 하면 과소적합, 적게 하면 과대적합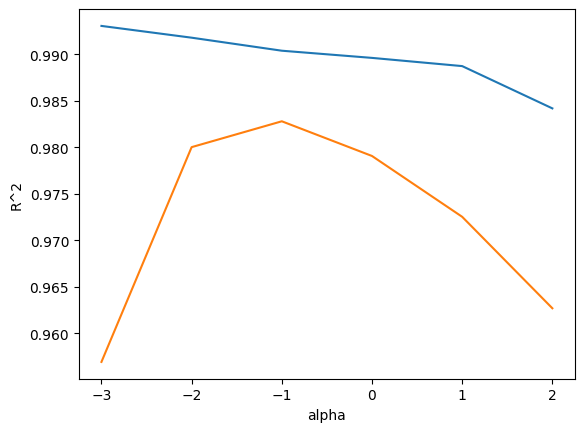
따라서, 최적의 alpha는 0.1이다.
3) 라쏘 (Lasso)
|가중치|로 규제 (= L1 규제)
마찬가지로 alpha를 통해 규제 강도를 조절한다.
하지만, 라쏘의 단점은 일부 특성을 사용하지 않는 경우가 많다는 것이다. (가중치가 0일 때 특성이 무시됨)
print(np.sum(lasso.coef_ == 0)) # true의 개수
# 40 (55개의 특성 中)5. 로지스틱 회귀
* 분류 알고리즘의 확률 = 특정 클래스일 확신
로지스틱 함수를 이용한 대표적인 분류 알고리즘
1) 이진 분류
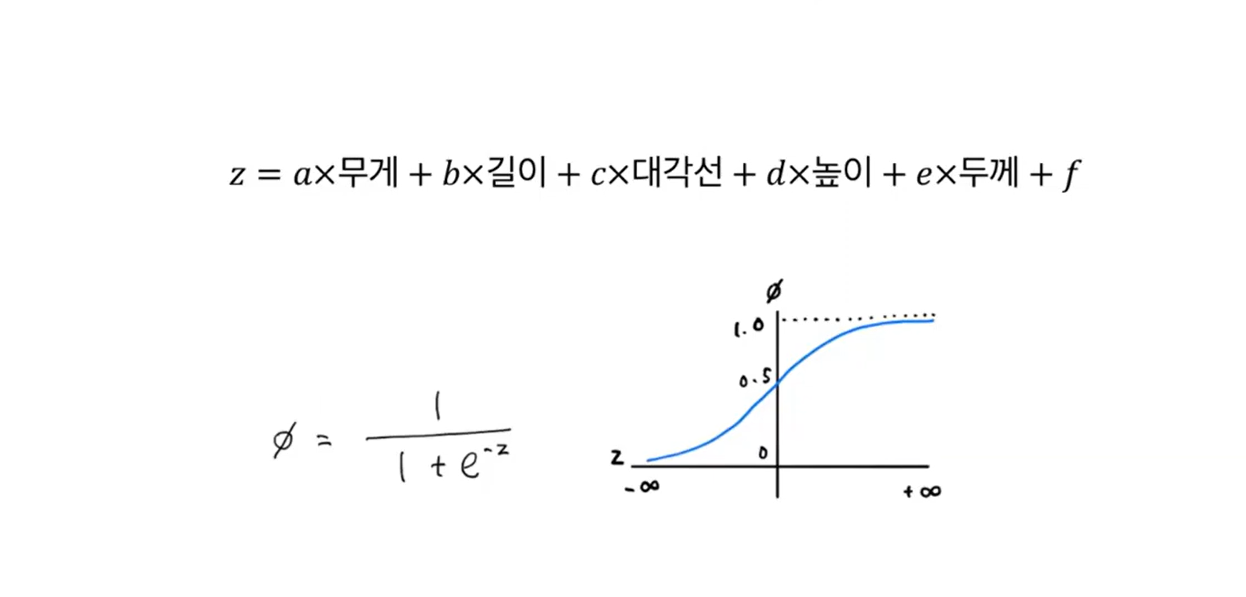
: 시그모이드 함수를 이용하여 확률값 계산
예시) 특성: Bream(도미), Smelt(빙어)
from sklearn.linear_model import LogisticRegression
lr = LogisticRegression()
lr.fit(train_bream_smelt, target_bream_smelt)
print(lr.predict(train_bream_smelt[:5]))
# ['Bream' 'Smelt' 'Bream' 'Bream' 'Bream']
print(lr.predict_proba(train_bream_smelt[:5])) # 1열: 음성(0=도미), 2열: 양성(1=빙어)일 확률
# [[0.99759855 0.00240145]
# [0.02735183 0.97264817]
# [0.99486072 0.00513928]
# [0.98584202 0.01415798]
# [0.99767269 0.00232731]]decisions = lr.decision_function(train_bream_smelt[:5]) # z값 반환
from scipy.special import expit
print(expit(decisions)) # 시그모이드 함수를 거친 확률 (양성 클래스만)
# [0.00240145 0.97264817 0.00513928 0.01415798 0.00232731]expit()은 양성 클래스에 대한 확률만 반환하기 때문에, 음성 클래스는 1을 빼서 구해야 한다.
2) 다중 분류
: 소프트맥스 함수를 이용하여 확률 표현
OVR (One VS Rest) : 이진 분류 모델을 사용해 다중 분류를 수행하는 방법
=> 각 클래스마다 선형 함수가 생성되어, 해당 클래스는 양성으로 두고 나머지는 음성으로 한 뒤 이진 분류 여러 번 실행 -> 클래스 개수만큼의 z가 생성되어 소프트맥스 함수에 넣고 확률로 변환
예시) 특성: Bream, Parkki, Perch, Pike, Roach, Smelt, Whitefish
# C: L2 Norm 규제 강도, 기본값 1 (alpha처럼) -> 숫자가 크면 강도 약해짐
lr = LogisticRegression(C=20, max_iter=1000) # max_iter: 반복 횟수 (기본값 100)
lr.fit(train_scaled, train_target)
print(lr.predict(test_scaled[:5]))
proba = lr.predict_proba(test_scaled[:5])
# ['Perch' 'Smelt' 'Pike' 'Roach' 'Perch']
print(np.round(proba, decimals=3))
# [[0. 0.014 0.841 0. 0.136 0.007 0.003]
# [0. 0.003 0.044 0. 0.007 0.946 0. ]
# [0. 0. 0.034 0.935 0.015 0.016 0. ]
# [0.011 0.034 0.306 0.007 0.567 0. 0.076]
# [0. 0. 0.904 0.002 0.089 0.002 0.001]]decision = lr.decision_function(test_scaled[:5]) # z값 반환
from scipy.special import softmax
proba = softmax(decision, axis=1)
# s1 = e^z1 / e_sum, ... , s7 = e^z7 / e_sum
print(np.round(proba, decimals=3))
# [[0. 0.014 0.841 0. 0.136 0.007 0.003]
# [0. 0.003 0.044 0. 0.007 0.946 0. ]
# [0. 0. 0.034 0.935 0.015 0.016 0. ]
# [0.011 0.034 0.306 0.007 0.567 0. 0.076]
# [0. 0. 0.904 0.002 0.089 0.002 0.001]]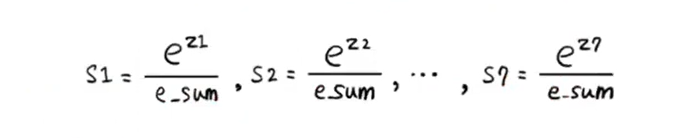
⭐ 요약
1. 지도 학습은 분류와 회귀로 나뉘는데 분류는 클래스를, 회귀는 임의의 숫자를 예측하는 것이다.
2. 과대적합은 훈련 데이터에 너무 최적화되어 모델이 복잡한 상태이고, 과소적합은 훈련 데이터의 패턴을 충분히 반영하지 못하는 상태이다.
3. 선형 회귀는 기울기와 절편으로 이루어진 방정식을 사용한다.
4. 다중 회귀는 특성이 여러 개이고, 다항 회귀는 차수를 높이는 것이다.
5. 규제는 기울기(가중치)를 조절하는데, 그중에서 릿지(Ridge)는 가중치의 제곱, 라쏘(Lasso)는 가중치의 절댓값을 사용해서 규제한다.
+ 규제를 많이 하면 과소적합, 적게 하면 과대적합이 발생한다.
6. 로지스틱 회귀에서 이진 분류는 시그모이드 함수를, 다중 분류는 소프트맥스 함수를 이용하여 확률을 표현한다.
* 참고자료: 혼자 공부하는 머신러닝+딥러닝 (박해선)
'Group Study (2023-2024) > Machine Learning 입문' 카테고리의 다른 글
| [ML입문] week6 - 순환 신경망 (1) | 2023.12.11 |
|---|---|
| [ML입문] week5 - 딥러닝 (0) | 2023.12.04 |
| [ML입문] week4 - 비지도 학습 (1) | 2023.11.27 |
| [ML입문] week3 - 분류 알고리즘(2), 트리 알고리즘 (0) | 2023.11.21 |
| [ML입문] week1 - 나의 첫 머신러닝, 데이터 다루기 (1) | 2023.11.06 |