학습 링크
https://www.edwith.org/ai216/joinLectures/132203
딥러닝 2단계: 심층 신경망 성능 향상시키기 강좌소개 : edwith
- Andrew Ng
www.edwith.org
https://www.edwith.org/ai218/joinLectures/138357
딥러닝 4단계: 합성곱 신경망 네트워크 (CNN) 강좌소개 : edwith
- Andrew Ng
www.edwith.org
PART 1. Setting up you ML application
Applied ML is a highly iterative process
- 신경망을 훈련시킬 때는 많은 결정을 내려야함.
- 신경망이 몇 개의 층을 가지는지
- 각각의 층이 몇 개의 은닉 유닛을 가지는지
- 학습률은 무엇인지
- 서로 다른 층에 사용하는 활성화 함수는 무엇인지
- ⇒ 이때 훈련, 개발, 테스트 세트를 잘 설정해 과정을 효율적으로 만들 수 있음.
Train/dev/test sets
- 머신러닝 이전의 시대에는
- 70 훈련 / 30 테스트 세트로 나누는 것이 일반적
- 60 테스트 / 20 개발 / 20 테스트 세트로 나눔
- 총 100만 개 이상의 샘플이 있는 현대 빅데이터 시대에는
- 개발세트와 테스트 세트가 훨씬 더 작은 비율이 되는게 트렌드
- 개발 세트와 테스트 세트의 목표 : 서로 다른 알고리즘을 확인, 어떤 알고리즘이 더 잘 작동하는지 확인하는 것
- 개발세트는 평가할 수 있을 정도로만 크면 됨
- 테스트 세트는 최종 분류기가 어느 정도 성능인지 신뢰 있는 추정치를 제공하는 것이므로 백만개가 있으면 만개만 해도 괜찮음
- 98 훈련 / 1 개발 / 1 테스트
- 백만개보다 더 많은 샘플을 가지는 경우 99.5 / 0.25 / 0.25 등으로 설정할 수 있음
- 머신러닝문제를 설정할 때는 훈련, 개발, 테스트 세트를 설정하게 되는데
- 이는 반복을 더 빠르게 함 → 알고리즘의 편향과 분산을 효율적으로 측정
- 상대적으로 적은 데이터 세트인 경우, 전통적인 비율로 설정하도 괜찮음.
- 훨씬 더 큰 경우라면 개발과 테스트 세트를 전체의 20 혹은 10보다 더 작게 설정하는 것도 괜찮은 방법
Mismatched train/test distribution
- 현대 딥러닝의 또 다른 트렌드는 더 많은 사람이 일치하지 않는 훈련 테스트 분포에서 훈련시킨다는 것
- 사용자가 모든 사진들을 업로드하는 앱을 만든다고 가정 → 고양이 사진을 찾아서 보여주는 것개발 / 테스트 세트 : 앱을 사용하는 사용자들에 의해 구성된 것 → 저해상도의 사진, 일상적
- ⇒ 두 세트의 데이터 분포는 달라질 수 있음.
- 훈련 세트 : 인터넷에서 다운 받은 고양이 사진
- 개발 세트가 테스트 세트와 같은 분포에서 오는 것이 좋음.
- why? 개발 세트를 사용해 다양한 모델을 평가하고 성능을 개선하기 위해 노력할 것이므로
- but, 딥러닝 알고리즘은 대량의 훈련 데이터가 필요하기 때문에 웹페이지를 크롤링함.
- 테스트 세트를 갖지 않아도 괜찮음.
- 테스트 세트의 목표 : 최종 네트워크의 성능에 대한 비편향 추정을 제공하는 것
- but, 비편향 추정이 필요 없는 경우에 테스트 세트를 갖지 않아도 괜찮음.
- 개발 세트만 있는 경우,
- 모든 테스트 세트를 훈련 세트에서 훈련시키고 다른 모델 아키텍트를 시도하고 이것을 개발 세트에서 평가 → 이 과정을 반복해서 좋은 모델 찾음.
- 개발 세트에 데이터를 맞추기 때문에 성능에 대한 비편향추정을 주지 않음.
- 그 추정이 필요하지 않다면, 테스트 세트가 없어도 괜찮음.
- 훈련 세트와 개발 세트만 있는 경우, 개발 세트를 테스트 세트라고 부름.
- 실제로는 테스트 세트를 교차 검증 세트로 사용하는 것
- 완벽히 좋은 용어는 아님. 테스트 세트에 과적합하기 때문.
Bias/Variance
- 편향 - 분산 트레이드오프

- 훈련 세트와 개발 세트의 관계
- 이 분석은 인간 수준의 성능이 거의 0% 라는 가정에 근거 ⇒ 최적의 오차, 베이지안 오차라고 불리는 베이지안 오차가 거의 0%라는 가정
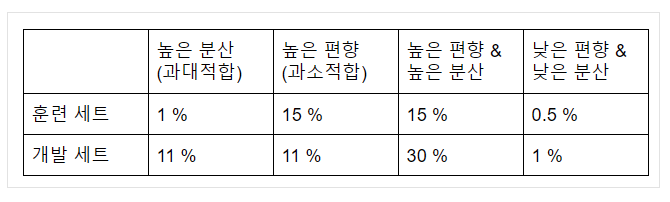
- 훈련 세트의 오차를 확인함으로써 최소한 훈련 데이터에서 얼마나 알고리즘이 적합한지에 대한 감을 잡을 수 있음 → 편향 문제가 있는지 확인 가능
- 훈련 세트에서 개발 세트로 갈 때 오차가 얼마나 커지는지 → 분산 문제가 얼마나 나쁜지 감을 잡을 수 있음.
Basic RECIPE for ML
- 정규화 : 분산을 줄이는데 매우 유용한 기술
- 편향을 조금 증가 → 약간의 편향 - 분산 트레이드오프
- 충분히 큰 네트워크가 있다면 크게 증가하지는 않음

PART2. Regularizing your neural network
Regularization
- 높은 분산으로 신경망이 데이터를 과대적합하는 문제가 의심된다면,
- 가장 먼저 정규화 시도 → 과대적합을 막고 신경망의 분산을 줄이는데 도움
- 더 많은 훈련 데이터를 얻는 것 → 비용이 많이 들어감
- L1보다는 L2 정규화를 보통 많이 사용
- 정규화는 훈련 속도를 빠르게 하고 모델에 어떠한 해도 가하지 않기 때문에 웬만하면 하는 게 좋음.

Why Regularization Reduces Overfitting
- λ 값을 크게 만들어서 가중치행렬 w 를 0에 가깝게 설정할 수 있음.
- 많은 은닉 유닛을 0에 가까운 값으로 설정 → 더 간단하고 작은 신경망
- tanh 활성화 함수를 사용할 경우 λ 값이 커지면, 비용함수에 의해 w는 작아지게 되고, 이때 z^[l] = w^[l]a^[l-1]+b^[l]이므로 z도 작아지게 됨.
- z 가 작을 때 g(z)는 선형 함수가 되고, 전체 네트워크도 선형이 되기에 과대적합과 같이 복잡한 결정을 내릴 수 없음.

Dropout Regularization
- 드롭아웃 : 신경망의 각각의 층에 대해 노드를 삭제하는 확률을 설정하는 것
- 삭제할 노드를 랜덤으로 선정 후 삭제된 노드의 들어가는 링크와 나가는 링크를 모두 삭제
- 그럼 더 작고 간소화된 네트워크가 만들어지고 이때 이 작아진 네트워크로 훈련을 진행
- 역 드롭아웃 : 노드를 삭제후에 얻은 활성화 값에 keep.prop을 나눠 주는 것
- 이는 기존에 삭제하지 않았을 때 활성화 값의 기대값으로 맞춰주기 위함
Understanding Dropout
- 드롭아웃은 무작위로 신경망의 유닛을 삭제 → 하나의 특성에 의존하지 못 하게 함 → 가중치를 다른 곳으로 분산 → 가중치의 노름의 제곱값이 줄어들게 됨.
- 드롭아웃의 keep.prop 확률은 층마다 다르게 설정할 수 있음.
- 모든 반복에서 잘 정의된 비용함수가 하강하는지 확인하는게 어려워짐. → 우선 드롭아웃을 사용하지 않고, 비용함수가 단조감소인지 확인 후에 사용
Other Regularization Methods
- L2 정규화와 드롭아웃 정규화와 더불어 신경망의 과대적합을 줄이는 다른 기법들
- Data Augmentation (데이터 증식)
- 이미지 → 더 많은 훈련 데이터 사용 ex) 대칭, 확대, 왜곡, 회전
- 독립적인 샘플을 얻는 것보다 많은 정보를 추가해주진 않지만, 컴퓨터적인 비용이 들지 않고 할 수 있음.
- 시각적인 문자의 인식 → 숫자를 얻어 무작위의 회전과 왜곡 부여
- 이미지 → 더 많은 훈련 데이터 사용 ex) 대칭, 확대, 왜곡, 회전
- Early Stopping (조기 종료)
- 훈련 오차나 비용함수 J는 단조 하강하는 형태
- 개발 세트의 오차도 그려줌
- 개발 세트 오차가 어느 순간부터 하락하지 않고 증가하기 시작하는 것 → 과대적화되는 시점
- ⇒ 조기 종료는 신경망이 개발 세트의 오차 저점 부근, 가장 잘 작동하는 점을 때 훈련을 멈춤.
- But, 조기 종료는비용 함수를 최적화 시키는 작업과 과대적합하지 않게 만드는 작업을 섞기 때문에 최적의 조건을 찾지 못 할 수 있음.
- Data Augmentation (데이터 증식)
PART3. Multi-class Calssification
Softmax Regression
Softmax : 여러 개의 클래스 분류 시 사용
- ex) Recognizing cats, dogs, and baby chicks
- Softmax 층을 통해 마지막 층 출력값이 주어졌을 때 해당 클래스에 속할 확률을 구할 수 있음.
- Softmax 층의 활성화 함수는
- t = e^(z^[L]) 이라는 임시 변수를 사용
- 모든 값들의 합이 1이 될 수 있도록 모든 임시 변수값들의 합을 나눠서 정규화
- 정규화를 하기 위해 입력값과 출력값이 모두 벡터
- Softmax 층의 활성화 함수는
Training a Softmax Classifier
- 소프트맥스라는 이름은 하드맥스와 반대되는 뜻
- 하드맥스 : z의 원소를 살펴보고 가장 큰 값이 있는 곳에 1을, 나머지에는 0을 갖는 벡터로 대응
- 반면, 소프트맥스는 z를 확률들로 대응
- 하드맥스 : z의 원소를 살펴보고 가장 큰 값이 있는 곳에 1을, 나머지에는 0을 갖는 벡터로 대응
- 소프트맥스 출력층을 이용해 신경망을 학습하는 법
- 손실함수
- 학습 알고리즘이 경사하강법을 이용해서 이 손실 함수의 값을 작게 만드려고 하니 결국 -logy^_2 값을 작게 만드는 것
- 결국 y^_2의 값을 가능한 한 크게 만들어야 함. → 이 값들이 확률이므로 1보다 커질 수 없음.
- ⇒ 훈련 세트에서 관측에 따른 클래스가 뭐든 간에 그 클래스에 대한 확률을 가능한 한 크게 만드는 것
- 비용함수 J
- 매개변수를 설정할 때 전체 훈련 세트에서 학습 알고리즘의 예측에 대한 훈련 샘플의 손실 함수를 합하는 것 → 이를 최소로 하기 위해 경사하강법 사용
- 손실함수
- Softmax 와 손실함수를 결합한 역전파의 값
- dz^[L] = y^−y
PART4. Convolutional Neural Networks
Computer Vision
- 컴퓨터 비전은 다양한 분야에 응용되고 있음.
- 주로 이미지 분류, 객체 인식, 신경망 스타일 번형 등
- but, 입력데이터가 아주 크다는 것 → 합성곱 연산을 통해 해결 가능
Edge detection Example
- 합성곱 작업 : 합성곱 신경망의 핵심 요소
- 합성곱 연산
- 원래 이미지 / 3*3 : 필터(커널) → 각각의 원소곱 후 전부 더해줌
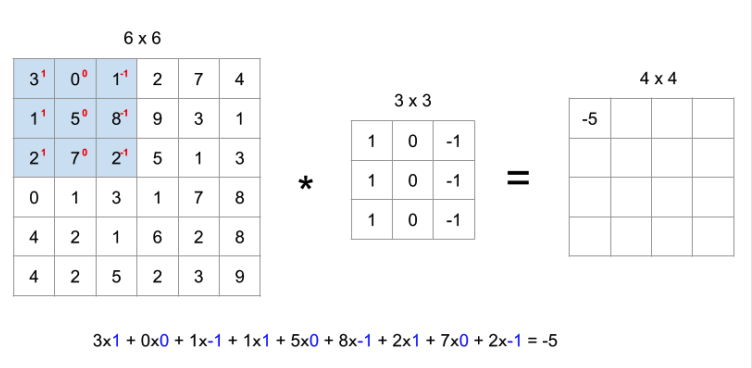
- 필터(커널)을 한칸 이동하여 합성곱 연산 진행 → 최종 4x4 새로운 행렬

- 원래 이미지 / 3*3 : 필터(커널) → 각각의 원소곱 후 전부 더해줌
- 수직 윤곽선 탐지법
- 10과 0사이의 경계선이 수직 윤곽선
- 필터를 통과해 합성곱 연산을 하게 되면 밝은 부분이 중앙으로 나타남. → 원래 이미지의 경계선

- 합성곱 연산
More Edge Detection
- 양과 음의 윤곽선 차이 → 서로 다른 밝기의 전환

Padding
- 합성곱 방식의 단점 두 가지
- 합성곱 연산을 거듭할수록 이미지는 축소됨
- 가장자리 픽셀은 단 한 번만 사용됨 → 이미지 윤곽쪽의 정보를 버리게됨
- 합성곱 방식의 단점을 해결하기 위해 패딩 사용
- 이미지 주위에 하나의 경계를 덧대는 것 → 이미지 크기가 커지므로 보통 숫자 0 사용
- 최종 이미지 크기: (n + 2p - f + 1) x (n + 2p - f + 1)
- n : 이미지 크기 / p : 패딩 크기 / f : 필터 크기
- 일반적으로 필터의 크기는 홀수
- 패딩이 비대칭 되기 때문. 홀수일 때 합성곱에서 동일한 크기로 패딩을 더해줄 수 있음.
- 중심위치가 존재하기 때문
Strided Convolutions
- 스트라이드 합성곱 : 합성곱 신경망의 기본 구성 요소
- 스트라이드 : 필터의 이동횟수 → 스트라이드를 주게 되면 그 수만큼 필터가 이동해서 계산
- 최종 크기 : ((n+2p-f)/s+1) * ((n+2p-f)/s+1)
Convolutions over volumes
- 이미지에 RGB가 들어가면 입체형으로변하게 되며, 차원이 하나 증가
- 높이 x 넓이 x 채널로 변함 → 채널은 색상 또는 입체형의 이미지의 깊이
- 합성곱에 사용되는 하나의 필터도 각 채널 별로 하나씩 증가
- 입체 이미지의 합성곱 계산 : 모든 채널의 합성곱 연산을 더해주는 형식
- 각 채널 별로 필터는 모두 같을 수 있고, 다를 수 있음
- 패딩과 스트라이드가 없다고 가정했을 때, 최종 출력은n: 이미지크기, n(c): 채널의 수, f: 필터의 크기, n(c'): 사용된 필터의 개수
- (n * n * n(c)) * ( f * f * n(c')) = (n - f + 1) * (n - f + 1) * n(c')
One Layer of a Convolutional Net
- 합성곱 신경망 한 계층의 구성 : 합성곱 연산 → 편향 추가 → 활성화 함수(비선형성을 적용하기 위함)

A Simple Convolution Network Example

- 신경망 층의 구성
- 합성곱 층
- 풀링 층
- 완전 연결 층
Pooling Layers
- 풀링 층 사용 → 표현의 크기 줄임 → 계산 속도 줄임 → 특징 더 잘 검출 가능
- 최대 풀링, 평균 풀링. 주로 최대 풀링 사용.

CNN Example
- LeNet-5 라는 사용한 고전적인 신경망과 유사한 구조

- 합성곱 신경망의 분야에는 두 종류의 관습
- 합성곱 층과 풀링 층을 하나의 층으로 간주 → 사용!
- 합성곱 층과 풀링 층을 각각의 층으로 간주

- Point
- 최대 풀링 층은 변수가 따로 없음
- 합성곱 층이 상대적으로 적은 변수를 가짐 (신경망의 대부분의 변수는 완전 연결 층에 있음)
- 활성값의 크기도 신경망이 깊어질수록 점점 감소
- Point
Why Convolutions
- 변수 공유
- 어떤 한 부분에서 이미지 특성 검출하는 필터가 이미지의 다른 부분에서도 똑같이 적용되거나 도움됨
- 희소 연결
- 출력값이 이미지의 일부의 영향을 받음. 나머지 픽셀들은 영향을 받지 않음. → 과대 적합 방지 가능
- 이동불변성을 포착하는데 용이
- 이미지가 약간의 변형이 있어도 포착 가능
'Group Study (2021-2022) > Machine Learning (GAN)' 카테고리의 다른 글
| [Machine Learning] 6주차 스터디-조건부 GAN (0) | 2021.11.22 |
|---|---|
| [Machine Learning] 5주차 스터디-합성곱 GAN (0) | 2021.11.12 |
| [Machine Learning] 3주차 스터디 - 파이토치와 신경망 기초 (0) | 2021.11.08 |
| [Machine Learning] 4주차 스터디-튼튼한 GAN 만들기 (0) | 2021.10.31 |
| [Machine Learning] 1주차 스터디 - 신경망과 딥러닝 (0) | 2021.10.04 |