스탠포드대학에서 발표한 CNN 강의 영상을 듣고 자료를 정리했습니다.
| Lecture 3 | Loss Functions and Optimization https://youtu.be/h7iBpEHGVNc |
| Lecture 4 | Introduction to Neural Networks https://youtu.be/d14TUNcbn1k |
Lecture 3 | Loss Functions and Optimization
loss function이란?
score에 대해 불만족하는 정도를 정량화 한 것이다.
SVM(Support Vetor Machine)의 loss function
SVM
기계학습 분야 중 하나로 패턴 인식, 자료 분석을 위한 지도 학습 모델이며, 분류, 회귀분석에 사용
고차원에서 결정경계를 기준으로 데이터를 분류
Support Vectors
결정 경계와 인접한 포인트들
Margin
서포트 벡터와 Decision boundary 간의 거리
Hinge loss function
허용가능한 오류 범위 내에서 가능한 최대 마진을 만들어야한다.

고양이 클래스의 점수를 보면 cat보다 car의 점수가 높다 → 잘못 분류
SVM loss function 계산과정


xi: 이미지, yi: 레이블, s: 레이블의 점수, 그 중 sj: 잘못된 레이블의 점수, syi: 제대로된 레이블의 점수
잘못된 레이블 스코어에서 제대로 된 레이블간 스코어 차에 일을 더한값이 영보다 크면 그 값이 loss가 되고 0보다 작으면 0이 레이블이 된다

세 개에 사진에 대해 Loss값(2.9, 0, 12.9)을 구하고 각 Li값을 합산하여 class의 개수(3)로 나눈다. → 5.27
SVM의 loss function특징
SVM은 데이터에 둔감하고, score값보다 정답 클래스가 다른 클래스보다 큰지 작은지 중요하다
loss는 0부터, 무한대까지 값을 가질 수 있다.
따라서 특정 가중치가 너무 과도하게 커지지 않도록 정규화(Regularization)항 추가해 사용한다.


L2 regularization
가중치가 전반적으로 작고 고르게 분산된 형태로 진행되어 과적합을 줄일 수 있다.
test set에 대한 일반적인 성능을 향상시킬 수 있게 된다.
Soft Max의 loss function
soft max
신경망 출력층에서 사용하는 활성함수, 분류문제에 사용됨
점수 벡터를 클래스 별 확률로 변환하기 위해 사용
연산 과정

주어진 스코어에 대해 exp 연산을 취해 값을 구하고, 그 값을 모두 더한 값을 해당 클래스 스코어에 나눠준다.
마지막으로 -log 연산을 취해 최종 확률을 계산한다.
Optimization
optimization
loss function을 최소화하는 Weight 찾기
w가 변할때 Loss가 얼마큼 변하는지 알아봐야한다.
방법 2가지
1. Random Search
w의 위치 값을 무작위로 포인트를 찾는 방법
예측 정확도가 불안정 → 절대로 사용하지 않음
2. Gradient Descent
loss function의 경사를 따라 내려가는 방법
Numerical Gradient와 Analytic Gradient 두 가지 방법이 있다.
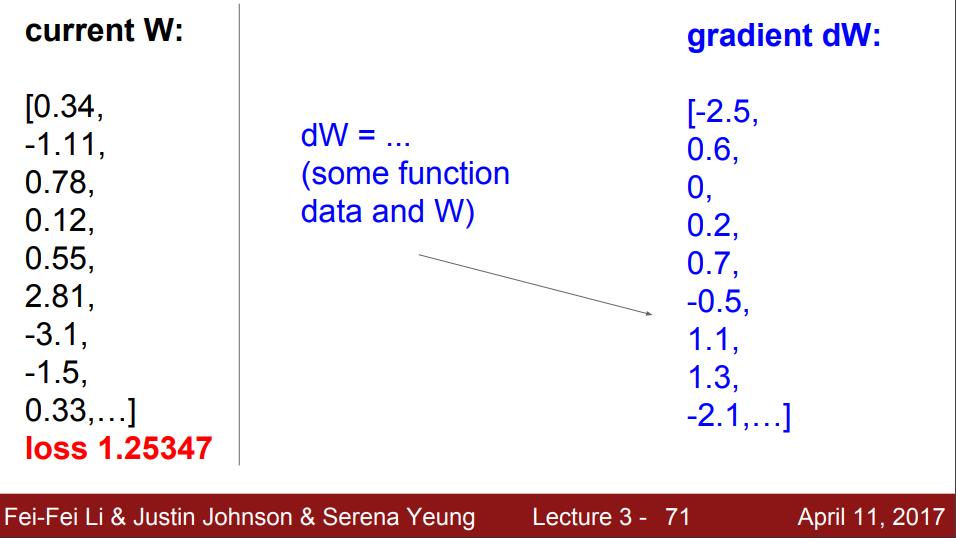
Numerical Gradient: 수치적으로 경사를 구하는 방법

h를 0.0001으로 미세하게 지정한 후f(x+h)의 loss를 구하면 1.2532가 나오고 이둘의 차를 0.0001로 나눈 경사값은 -2.5를 얻었다.
기울기가 음수라는건, 기울기가 w가 늘어나면 loss에 음의 영향을 준다는걸 의미한다.
기울기가 늘어나면 loss에 양의 영향을 가지고 있다고 의미한다.
loss의 변화가 없는것은 기울기가 없다는 것이다.
단점: 정확한 값이 아닌 근사값을 구한 것이라 값이 정확하지 않고, weight가 무수히 많을 경우 평가를 하기가 어렵고 값을 구하기에도 느리다.
Analytic Gradient: 미분을 통해 경사를 구하는 법
미분식을 이용하면 다음과 같이 편미분값들을 구할 수 있다.
Gradient Check
실제로는 Analytic Gradient을 쓰면 되고 계산을 정확하게 이뤄냈는지 검토과정에서 Numerical Gradient 방법을 활용한다.
코드로 구현
1. Full Gradient Descent

loss function, data, weight 인자로 전달 → Gradient 구한다
구한 gradient에 stepsize(learing rate)를 곱하고 기존 weight에 추가하여 Weight를 업데이트 한다.
gradient 값만큼 weight를 감소시켜 주기 위해 앞에 마이너스 붙임
2. Mini-Batch Gradient Descent
현실적으로 많이 사용되는 방법
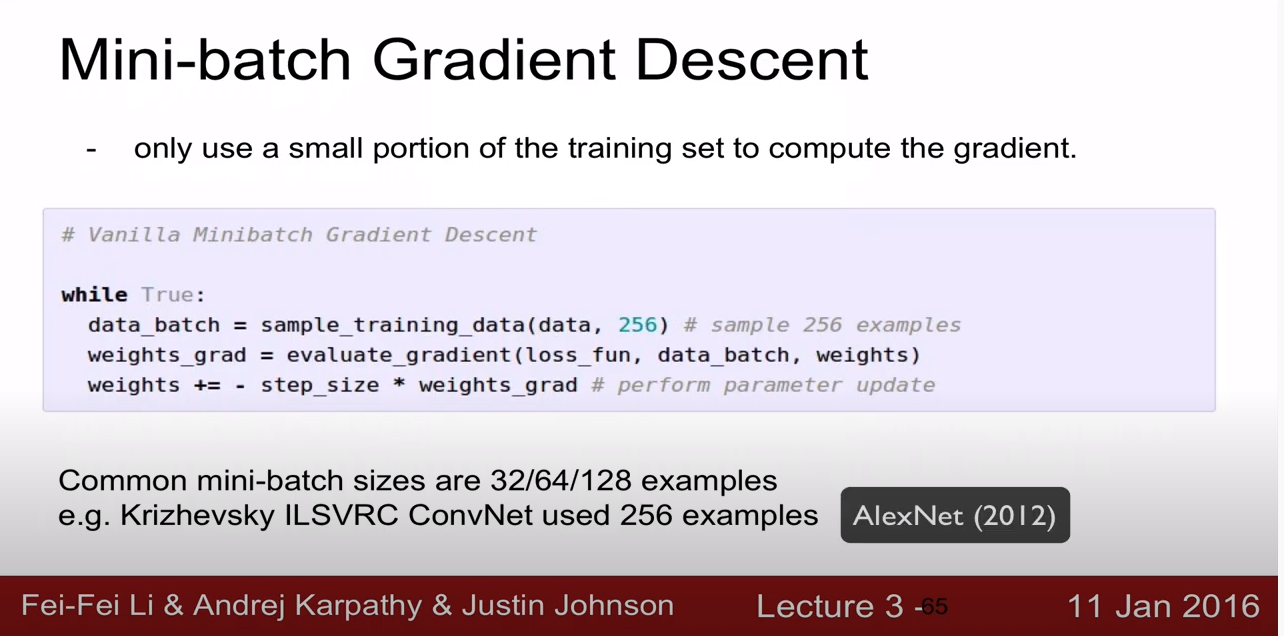
training set의 일부만 사용해서 gradient을 계산하고, parameter을 업데이트해주는데, 계속 또 다른 training set의 일부를 이용해 parameter을 업데이트 하는 방법을 계속해서 반복하는 과정이다.
Mini-Batch Gradient Descent 중 하나로 Stochastic Gradient Descent(SGD)가 있다.
Lecture 4 | Backpropagation and Neural Networks
Front Propagation
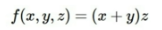
x, y, z값이 주어지고, 왼쪽에서 오른쪽 노드로 건너가며 연산이 진행
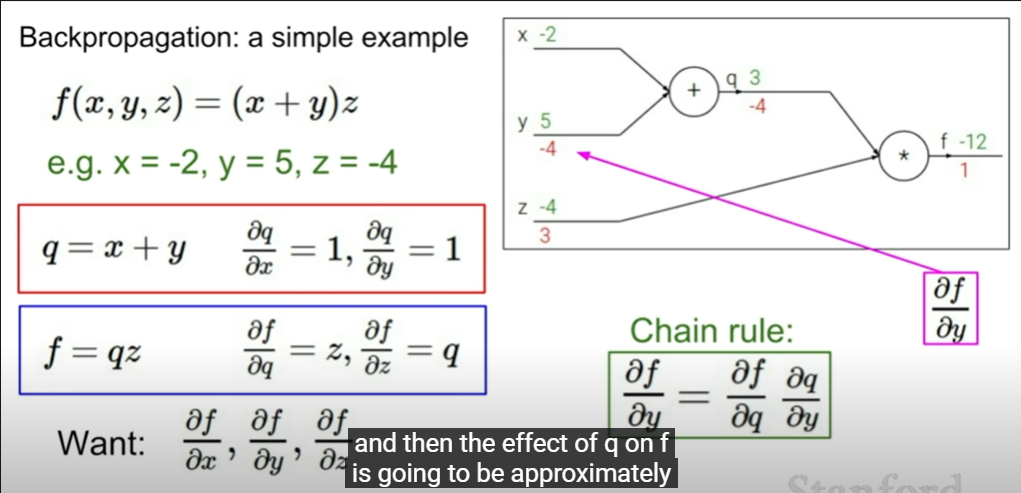
Back propagation
x, y, z가 f(x,y,z)에 어떠한 영향을 미치는지 알아보기 위해 backpropagation 연산을 활용
말 그대로 거꾸로 연산하는 것이다
뒤에서부터(마지막 연산부터) 편미분 진행
행렬 Back propagation연산은 다음과 같다
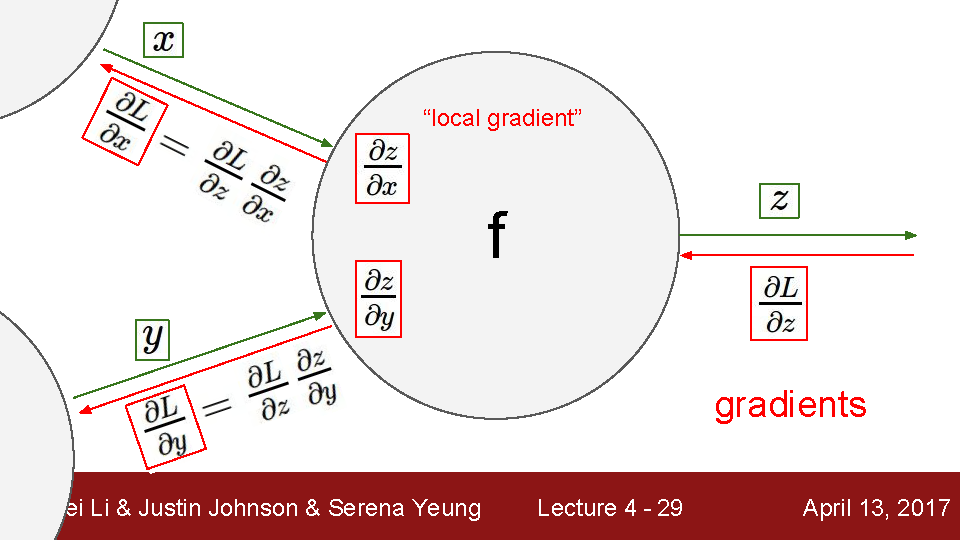



Jacobian Matrix
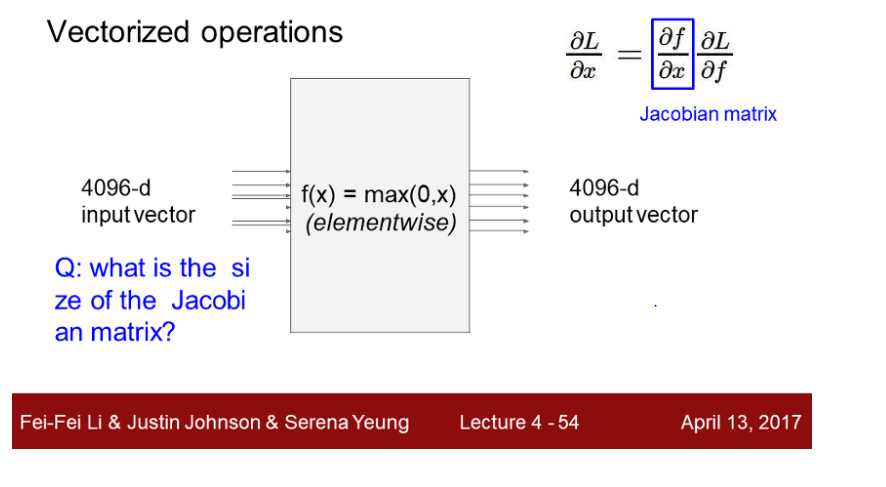
Jacobian 행렬은 해당 함수의 편도함수 행렬으로, local gradient * global gradient 연산을 할 때 필요한 매트릭스다.
Jacobian matrix크기는 4096 * 4096 으로 주어지면 minibatch 를 이용해 연산 시, 실용적이지 못하다. 따라서 연산하지 않고, 출력에 대한 x영향을 구할 때 max 연산을 통해 일부는 0으로 채운다.
Neurual Network
여러 겹층의 Linear Classifier로 구성된 것

지난번에 다룬 Linear Classifier의 f = wx에 hidden layer 가 추가 되었을시 , 3072의 데이터가 w1와 곱해지고 h노드(hidden layer)에 들어가고 다시 w2 가중치 연산을 통해 10개의 출력값으로 나온다.
hidden 노드에 따라 더 많은 Classifier를 생성할 수 있다.
다음 포스트에서는 Activation Function, Neural Network Architecture에 대해 다뤄볼 것이다.
'Group Study (2022-2023) > Machine Learning' 카테고리의 다른 글
| [Machine Learning] 3주차 스터디 - Softmax Regression (0) | 2022.10.31 |
|---|---|
| [Machine Learning] 4주차 스터디 - Application & Tips (0) | 2022.10.31 |
| [Machine Learning] 2주차 스터디 - Multi variable linear regression & Logistic Regression (0) | 2022.10.10 |
| [Machine Learning] 1주차 스터디 - CNN의 이해(1) (0) | 2022.10.06 |
| [Machine Learning] 1주차 스터디 - 머신러닝의 용어와 개념 & 선형 회귀(Linear Regression) (0) | 2022.10.04 |