7. 딥러닝
7.1.1. 인공신경망 :
- 생물학적 뉴런에서 영감을 받아 만든 머신러닝 알고리즘
- 인공신경망 알고리즘을 딥러닝이라고도 부름.
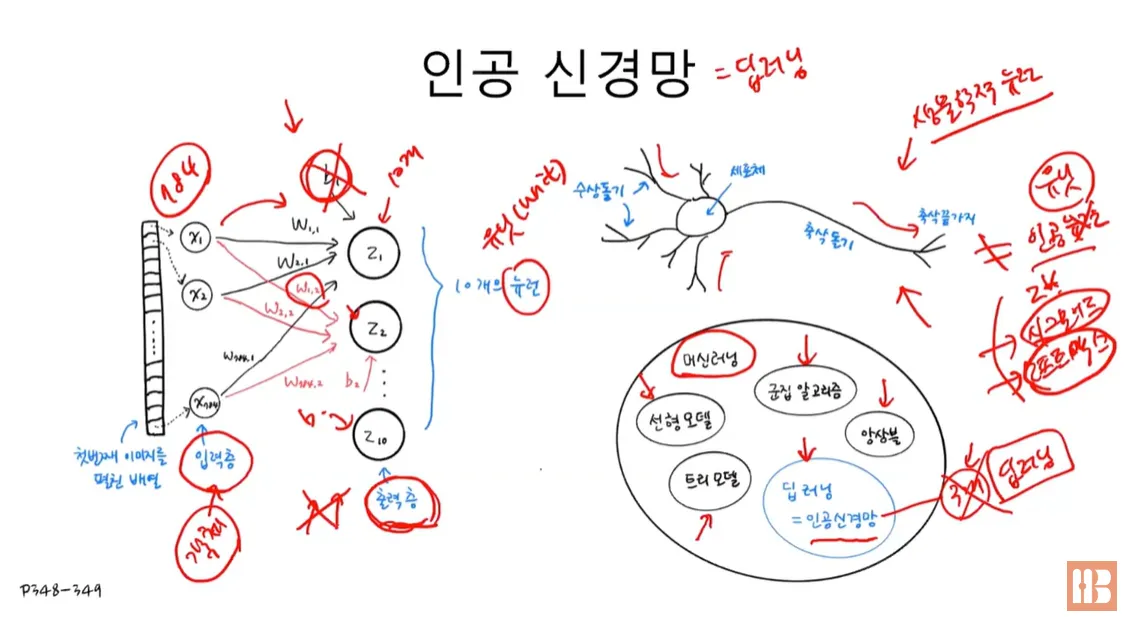
7.1.2 패션 MNIST 데이터셋 :
0~9까지 10개의 클래스 , 28*28 흑백 픽셀 , 6만개 데이터 사용.

7.1.3 텐서플로 (TensorFlow) :
구글이 만든 딥러닝 라이브러리. 의 ‘케라스 패키지’를 import.
- Dense : 신경망에서 가장 기본 층인 밀집층을 만드는 클래스.

- 첫 번째 매개변수에는 뉴런의 개수를 지정.
- activation 매개변수에는 사용할 활성화 함수를 지정하는데, 대표적으로 ‘sigmoid’, ‘softmax’ 함수가 있음.
- 아무것도 지정하지 않으면 활성화 함수를 사용하지 않음.
from tensorflow import keras
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
print(train_input.shape, train_target.shape) # 데이터 크기 확인 : (60000, 28, 28) (60000,)
print(test_input.shape, test_target.shape) # 테스트 세트의 크기 확인 : (10000, 28, 28) (10000,)import matplotlib.pyplot as plt
fig, axs = plt.subplots(1, 10, figsize=(10,10))
for i in range(10):
axs[i].imshow(train_input[i], cmap='gray_r') # 반전시켜 출력하기 위함
axs[i].axis('off')
plt.show()
print([train_target[i] for i in range(10)])
-> [9, 0, 0, 3, 0, 2, 7, 2, 5, 5]
print(np.unique(train_target, return_counts=True))
-> (array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000, 6000]))
7.1.4 로지스틱 회귀로 패션 아이템 분류하기

train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28) # 3차원 데이터를 하나의 차원으로
print(train_scaled.shape)
-> (60000, 784)
from sklearn.model_selection import cross_validate
from sklearn.linear_model import SGDClassifier
sc = SGDClassifier(loss='log_loss', max_iter=5, random_state=42)
# loss='log' = 10개 클래스 다중 분류. 10개의 이진분류 수행.
# ex) 부츠가 양성이면, 나머지 9개 클래스는 음성.
scores = cross_validate(sc, train_scaled, train_target, n_jobs=-1)
print(np.mean(scores['test_score']))
-> 0.8196000000000001
7.1.5 케라스 모델 만들기
케라스의 Sequential 클래스에 맨 처음 추가되는 층에는 input_shape 매개변수로 입력의 크기를 정해야 함.
- Sequential : 케라스에서 신경망 모델을 만드는 클래스.
- 이 클래스의 객체를 생성할 때, 신경망 모델에 추가할 층을 지정할 수 있음. 추가할 층이 1개 이상일 경우 파이썬 리스트로 전달.

7.1.6 밀집층 (dense 클래스 / 완전완결층) :
- dense = keras.layers.Dense(뉴런의 개수, 뉴런의 출력에 적용할 함수, 입력의 크기)
- 가장 간단한 인공 신경망의 층.
- 밀집층에서는 뉴런들이 모두 연결되어 있기 때문에 완전 연결층이라고도 부름.
- 특별히 출력층에 밀집층을 사용할 때는 분류하려는 클래스와 동일한 개수의 뉴런을 사용.
from sklearn.model_selection import train_test_split
train_scaled, val_scaled, train_target, val_target = train_test_split(
train_scaled, train_target, test_size=0.2, random_state=42)
print(train_scaled.shape, train_target.shape)
print(val_scaled.shape, val_target.shape)
-> (48000, 784) (48000,)
-> (12000, 784) (12000,)
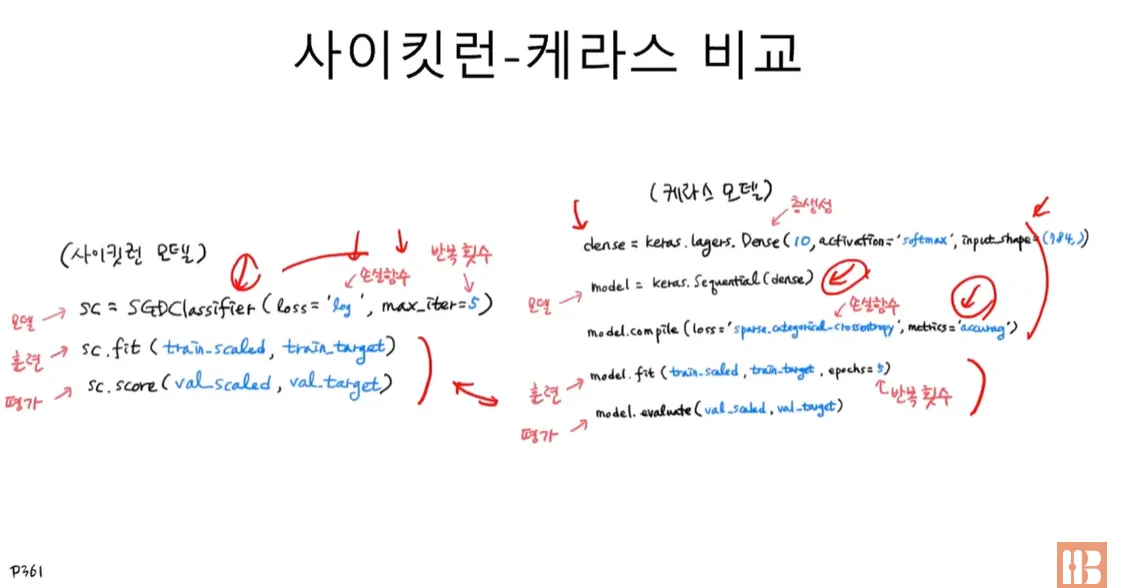
dense = keras.layers.Dense(10, activation='softmax', input_shape=(784,))
model = keras.Sequential([dense])
7.1.7 인공신경망으로 패션 아이템 분류하기
- 이진 분류 → loss : ‘binary-crossentropy’
- 다중분류 → loss : ‘categorical -crossentropy’

model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])
print(train_target[:10])
-> [7 3 5 8 6 9 3 3 9 9]
model.fit(train_scaled, train_target, epochs=5)
model.evaluate(val_scaled, val_target)- compile() : 모델 객체를 만든 후 훈련하기 전에 사용할 손실 함수와 측정 지표 등을 지정하는 메서드.
- loss 매개변수에 손실 함수를 지정하고, 이진 분류일 경우 ‘binary_crossentropy’ , 다중 분류일 경우 ‘categorical_crossentropy’ 를 지정.
- 클래스 레이블이 정수일 경우 ‘sparse_categorical_crossentropy’ 로 지정.
- 회귀 모델일 경우 ‘mean_squre_error’ 등으로 지정.
- metrics 매개변수에 훈련 과정에서 측정하고 싶은 지표를 지정할 수 있음. 측정 지표가 1개 이상일 경우 리스트로 전달.

- fit() : 모델을 훈련하는 메서드.
- 첫 번째와 두 번째 매개변수에 입력과 타깃 데이터를 전달.
- epochs 매개변수에 전체 데이터에 대해 반복할 에포크 횟수를 지정.
- evaluate() : 모델 성능을 평가하는 메서드
- 첫 번째와 두 번째 매개변수에 입력과 타깃 데이터를 전달.
- compile() 메서드에서 loss 매개변수에 지정한 손실 함수의 값과 metrics 매개변수에서 지정한 측정 지표를 출력.
7.1.8 사이킷런-케라스 비교
7.2.1 : 심층신경망
- 2개의 층 (입력층은 제하고 계산.)
- 2개 이상의 층을 포함한 신경망. 종종 다층 인공신경망, 심층 신경망, 딥러닝을 같은 의미로 사용.


from tensorflow import keras
(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
from sklearn.model_selection import train_test_split
train_scaled = train_input / 255.0
train_scaled = train_scaled.reshape(-1, 28*28)
train_scaled, val_scaled, train_target, val_target = train_test_split(
train_scaled, train_target, test_size=0.2, random_state=42)
dense1 = keras.layers.Dense(100, activation='sigmoid', input_shape=(784,))
dense2 = keras.layers.Dense(10, activation='softmax')model = keras.Sequential([dense1, dense2])
model.summary()`Model: "sequential"`
`┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ dense (Dense) │ (None, 100) │ 78,500 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense) │ (None, 10) │ 1,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘`
`Total params: 79,510 (310.59 KB)`
`Trainable params: 79,510 (310.59 KB)`
`Non-trainable params: 0 (0.00 B)`
7.2.2 summary() :
- 케라스 모델의 정보를 출력하는 메서드.
- 모델에 추가된 층의 종류와 순서, 모델 파라미터 개수를 출력.
- 층을 만들 때 name 매개변수로 이름을 지정하면 summary() 메서드 출력에서 구분하기 쉬움.

7.2.3. 층을 추가하는 방법 :
- add() : 케라스 모델에 층을 추가하는 메서드
- 케라스 모델의 add() 메서드는 keras.layers 패키지 아래에 있는 층의 객체를 입력받아 신경망 모데에 추가.
- add() 메서드를 호출하여 전달한 순서대로 층이 차례대로 늘어남.

model = keras.Sequential([
keras.layers.Dense(100, activation='sigmoid', input_shape=(784,), name='hidden'),
keras.layers.Dense(10, activation='softmax', name='output')
], name='패션 MNIST 모델')
model.summary()
->
`Model: "패션 MNIST 모델"`
`┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ hidden (Dense) │ (None, 100) │ 78,500 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ output (Dense) │ (None, 10) │ 1,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘`
`Total params: 79,510 (310.59 KB)`
`Trainable params: 79,510 (310.59 KB)`
`Non-trainable params:0 (0.00 B)`
7.2.4. 렐루 함수 :
- 이미지 분류 모델의 은닉층에 많이 사용되는 활성화 함수.
- 시그모이드 함수는 층이 많을수록 활성화 함수의 양쪽 끝에서 변화가 작기 때문에 학습이 어려움.
- 렐루 함수는 이런 문제가 없으며, 계산도 간단함.

model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()
->
`Model: "sequential_2"`
`┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ flatten (Flatten) │ (None, 784) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_6 (Dense) │ (None, 100) │ 78,500 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_7 (Dense) │ (None, 10) │ 1,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘`
`Total params: 79,510 (310.59 KB)`
`Trainable params: 79,510 (310.59 KB)`
`Non-trainable params: 0 (0.00 B)`
7.2.5 : 옵티마이저 (확률적 경사 하강법을 사용)
- 신경망의 가중치와 절편을 학습하기 위한 알고리즘 또는 방법.
- 케라스의 SGD, 네스테로프 모멘텀, RMSprop, Adam 과 같은 알고리즘이 예시.

(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
train_scaled = train_input / 255.0
train_scaled, val_scaled, train_target, val_target = train_test_split(
train_scaled, train_target, test_size=0.2, random_state=42)
model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])
model.fit(train_scaled, train_target, epochs=5)
-> Epoch 1/5
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 7s 4ms/step - accuracy: 0.7655 - loss: 0.6770
Epoch 2/5
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 9s 3ms/step - accuracy: 0.8553 - loss: 0.3962
Epoch 3/5
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 3ms/step - accuracy: 0.8715 - loss: 0.3530
Epoch 4/5
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 3s 2ms/step - accuracy: 0.8771 - loss: 0.3373
Epoch 5/5
1500/1500 ━━━━━━━━━━━━━━━━━━━━ 4s 2ms/step - accuracy: 0.8887 - loss: 0.3066
<keras.src.callbacks.history.History at 0x7da9f86622c0>
model.evaluate(val_scaled, val_target)
-> 375/375 ━━━━━━━━━━━━━━━━━━━━ 1s 3ms/step - accuracy: 0.8754 - loss: 0.3629
[0.3661682605743408, 0.8741666674613953]1. SGD : 기본 경사 하강법 옵티마이저 클래스.
- learning_rate 매개변수로 학습률을 지정, 기본값은 0.01
- momemtum 매개변수에 0 이상의 값 지정 → 모멘텀 최적화 수행
- nesterov 매개변수를 True로 설정 → 네스테로프 모멘텀 최적화를 수행
2. Adagard 옵티마이저 클래스 :
- learning_rate 매개변수로 학습률 지정, 기본값은 0.001
- Adagard 는 그레디언트 제곱을 누적하여 학습률을 나눔.
- initial_accumulator_value 매개변수에서 누적 초깃값을 지정할 수 있으며, 기본값은 0.1
3. RMSprop 옵티마이저 클래스 :
- learning_rate 매개변수로 학습률 지정. 기본값은 0.001
- 그레디언트 사용을 위해 지수 감소를 사용. rho 매개변수에서 감소 비율을 지정하며, 기본값은 0.9
4. Adam 옵티마이저 클래스 :
- learning_rate 매개변수로 학습률 지정. 기본값은 0.001
- 모멘텀 최적화에 있는 그레이디언트의 지수 감소 평균을 조절하기 위하여 beta_1 매개변수가 있으며 기본값은 0.9
- RMSprop에 있는 그레디언트 제곱의 지수 감소 평균을 조절. beta_2 매개변수가 있으며 기본값은 0.999
7.3.1 손실 곡선
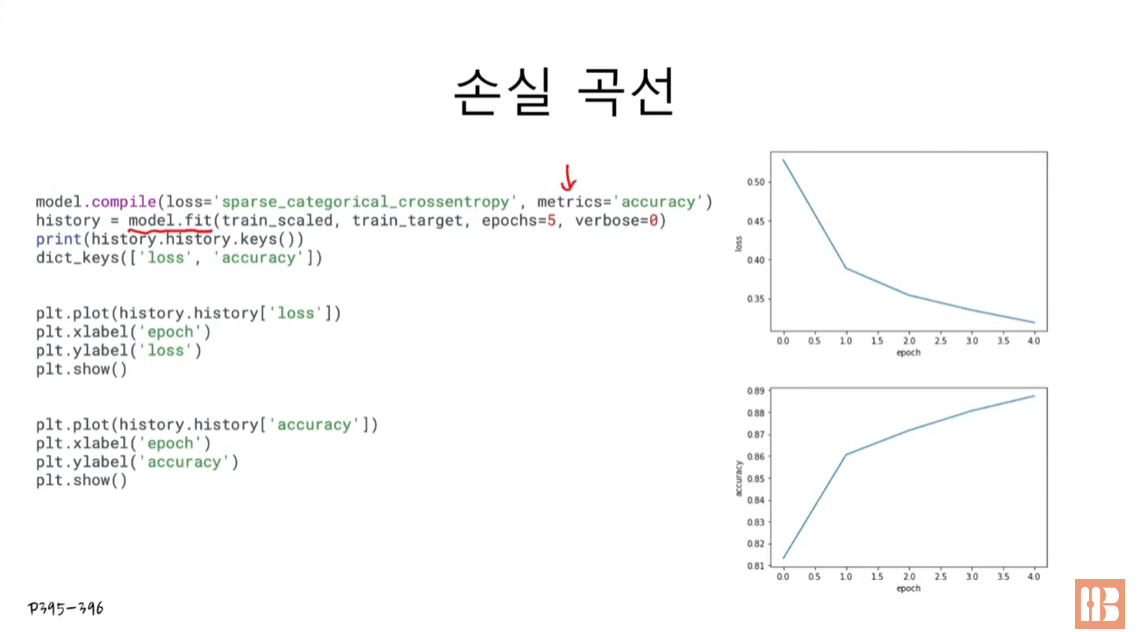

from tensorflow import keras
from sklearn.model_selection import train_test_split
(train_input, train_target), (test_input, test_target) = \
keras.datasets.fashion_mnist.load_data()
train_scaled = train_input / 255.0
train_scaled, val_scaled, train_target, val_target = train_test_split(
train_scaled, train_target, test_size=0.2, random_state=42)
def model_fn(a_layer=None):
model = keras.Sequential()
model.add(keras.layers.Flatten(input_shape=(28, 28)))
model.add(keras.layers.Dense(100, activation='relu'))
if a_layer:
model.add(a_layer)
model.add(keras.layers.Dense(10, activation='softmax'))
return model
model = model_fn()
model.summary()
-> Model: "sequential"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ flatten (Flatten) │ (None, 784) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense (Dense) │ (None, 100) │ 78,500 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_1 (Dense) │ (None, 10) │ 1,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 79,510 (310.59 KB)
Trainable params: 79,510 (310.59 KB)
Non-trainable params: 0 (0.00 B)model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])
history = model.fit(train_scaled, train_target, epochs=5, verbose=0)
print(history.history.keys())
-> dict_keys(['accuracy', 'loss'])import matplotlib.pyplot as plt
plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
plt.plot(history.history['accuracy'])
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])
history = model.fit(train_scaled, train_target, epochs=20, verbose=0)
plt.plot(history.history['loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()에포크마다 손실이 감소하고 정확도가 향상 -> 에포크를 늘려서 (20정도) 훈련 계속.

에포크에 대한 과대적합과 과소적합을 파악하려면 훈련 세트에 대한 점수 뿐만 아니라 검증 세트에 대한 점수도 필요. 따라서, 검증 데이터도 계산이 필요하다.
7.3.2 검증 손실
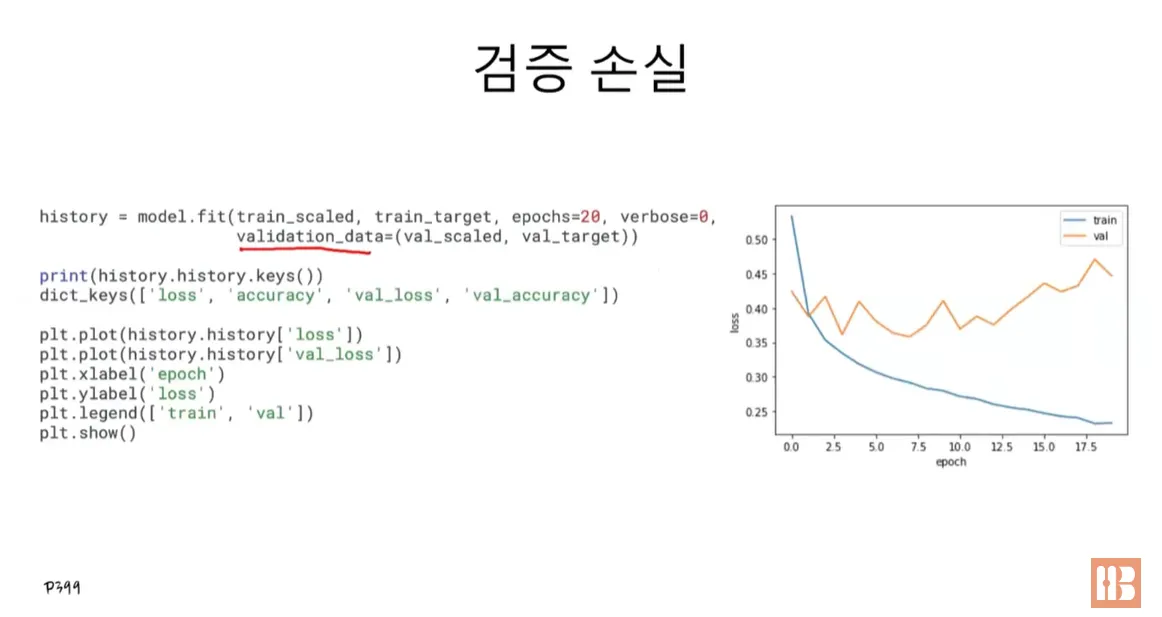
model = model_fn()
model.compile(loss='sparse_categorical_crossentropy', metrics=['accuracy'])
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target))
print(history.history.keys())
-> dict_keys(['accuracy', 'loss', 'val_accuracy', 'val_loss'])
-> 검증 세트에 대한 손실은 val_loss 에, 정확도는 val_accuracy 에 들어있음.
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
처음에는 검증 손실이 감소하다가 다섯 번째 에포크만에 다시 상승함.
훈련 손실은 꾸준히 감소하기 때문에, 검증 손실이 상승하는 시점을 뒤로 늦추면 검증 세트에 대한 손실이 줄어들며, 정확도가 증가할 것.
model = model_fn()
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
열 번째 에포크까지 전반적인 감소 추세 보임. Adam 옵티마이저가 데이터셋에 잘 맞는다는 것을 보여줌.
7.3.3 드롭아웃
- 은닉층에 있는 뉴런의 출력을 랜덤하게 껴서 과대적합을 막는 기법.
- 드롭아웃은 훈련 중에 적용되며, 평가나 예측에서는 적용되지 않음. 텐서플로는 이를 자동으로 처리함.


Dropout (드롭아웃 층) :
- 첫 번째 매개변수로 드롭아웃할 비율 (r)을 지정.
- 드롭아웃 하지 않는 뉴런의 출력은 1/(1-r)만큼 증가시켜 출력의 총합이 같도록 만든다.
model = model_fn(keras.layers.Dropout(0.3))
model.summary()
-> Model: "sequential_3"
┏━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┳━━━━━━━━━━━━━━━━━┓
┃ Layer (type) ┃ Output Shape ┃ Param # ┃
┡━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━━━━━━━━━━━━━╇━━━━━━━━━━━━━━━━━┩
│ flatten_3 (Flatten) │ (None, 784) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_6 (Dense) │ (None, 100) │ 78,500 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dropout (Dropout) │ (None, 100) │ 0 │
├──────────────────────────────────────┼─────────────────────────────┼─────────────────┤
│ dense_7 (Dense) │ (None, 10) │ 1,010 │
└──────────────────────────────────────┴─────────────────────────────┴─────────────────┘
Total params: 79,510 (310.59 KB)
Trainable params: 79,510 (310.59 KB)
Non-trainable params: 0 (0.00 B)
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target))
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
열 번째 에포크 정도에서 검증 손실의 감소가 멈추지만 크게 상승하지 않고 어느정도 유지되고 있다.
따라서, 이 모델은 20번의 에포크동안 훈련을 했기 때문에 다소 과대적합 되어 있다.
따라서, 과대적합 되지 않은 모델을 얻기 위해 에포크 횟수를 10으로 두고 다시 훈련해야 한다.
7.3.4 모델 저장과 복원

model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(train_scaled, train_target, epochs=10, verbose=0,
validation_data=(val_scaled, val_target))
model.save('model-whole.keras')
model.save_weights('model.weights.h5')
!ls -al model*
model = model_fn(keras.layers.Dropout(0.3))
model.load_weights('model.weights.h5')
-> -rw-r--r-- 1 root root 971928 Nov 10 12:25 model.weights.h5
-rw-r--r-- 1 root root 975719 Nov 10 12:25 model-whole.keras
import numpy as np
val_labels = np.argmax(model.predict(val_scaled), axis=-1)
print(np.mean(val_labels == val_target))
-> 0.8795
model = keras.models.load_model('model-whole.keras')
model.evaluate(val_scaled, val_target)
-> [0.33250948786735535, 0.8794999718666077]1. save_weights() :
- 모든 층의 가중치와 절편을 파일에 저장.
- 첫 번째 매개변수에 저장할 파일을 지정, save_format 매개변수에서 지정할 파일 포맷을 지정.
- 텐서플로의 Checkpoint 포맷을 사용.
2. load_weights() :
- 모든 층의 가중치와 절편을 파일에 읽음.
- 첫 번째 매개변수에 읽을 파일을 지정
3. save() :
- 모델 구조와 모든 가중치와 절편을 파일에 저장.
- 첫 번째 매개변수에 저장할 파일을 지정.
- save_format 매개변수에서 지정할 파일 포맷을 지정.
7.3.5 콜백 :
- 케라스 모델을 훈련하는 도중에 어떤 작업을 수행할 수 있도록 도와주는 도구.
- 대표적으로 최상의 모델을 자동으로 저장해주거나 검증 도구가 더 이상 향상되지 않으면 일찍 종료 가능.
7.3.6 조기 종료 :
- 검증 점수가 더 이상 감소하지 않고, 상승하여 과대적합이 일어나면 훈련을 계속 진행하지 않고 멈추는 기법.
- 계산 비용과 시간 절약 가능


model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.keras',
save_best_only=True)
model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target),
callbacks=[checkpoint_cb])
model = keras.models.load_model('best-model.keras')
model.evaluate(val_scaled, val_target)
-> [0.31556007266044617, 0.8859166502952576]
model = model_fn(keras.layers.Dropout(0.3))
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.keras',
save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2,
restore_best_weights=True)
history = model.fit(train_scaled, train_target, epochs=20, verbose=0,
validation_data=(val_scaled, val_target),
callbacks=[checkpoint_cb, early_stopping_cb])
print(early_stopping_cb.stopped_epoch)
-> 11
# 열 번째 에포크가 최적이라는 의미.
# 그래프에서 9로 나타나있는 부분을 보면, 가장 낮은 검증 손실을 가지고 있다.
# 열 두번째에서 훈련을 멈추었다.
plt.plot(history.history['loss'])
plt.plot(history.history['val_loss'])
plt.xlabel('epoch')
plt.ylabel('loss')
plt.legend(['train', 'val'])
plt.show()
model.evaluate(val_scaled, val_target)
-> [0.3249325454235077, 0.8849166631698608]
1. load_model() :
- model.save() 로 저장된 모델을 로드
- 첫 번째 매개변수에 읽을 파일 지정
2. ModelCheckpoint :
- 케라스 모델과 가중치를 일정 간격으로 저장
- 첫 번째 매개변수에 저장할 파일을 지정
- monitor 매개변수 : 모니터링할 지표를 지정 , 기본값은 ‘val_loss’ 로 검증 손실을 관찰
- save_weights_only 매개변수 기본값 : False , 전체 모델을 저장 → True 로 지정하면 모델의 가중치와 절편만 저장
- save_best_only 매개변수 True 로 지정 → 가장 낮은 검증 점수를 만드는 모델을 저장.
3. EarlyStopping :
- 관심 지표가 더 이상 향상하지 않으면 훈련을 중지.
- monitor 매개변수 : 모니터링할 지표를 지정, 기본값은 ‘val_loass’로 검증 손실을 관찰.
- patience 매개변수 : 모델이 더 이상 향상되지 않고 지속할 수 있는 최대 에포크 횟수를 지정.
- restore_best_weights 매개변수 기본값 : False
참고자료 :
1. 혼자 공부하는 머신러닝, 박해선, 한빛미디어
2. 혼자 공부하는 머신러닝 인프런 강의, 박해선, https://www.inflearn.com/course/%ED%98%BC%EC%9E%90%EA%B3%B5%EB%B6%80-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EB%94%A5%EB%9F%AC%EB%8B%9D/dashboard
'Group Study (2024-2025) > Machine Learning 입문' 카테고리의 다른 글
| [ML 입문] 8주차 스터디 (1) | 2024.11.27 |
|---|---|
| [ML 입문] 7주차 스터디 (1) | 2024.11.20 |
| [ML 입문] 5주차 스터디 (1) | 2024.11.06 |
| [ML 입문] 4주차 스터디 (0) | 2024.10.30 |
| [ML 입문] 3주차 스터디 (1) | 2024.10.16 |