8-1. 합성곱 신경망의 구성요소
밀집층
뉴런마다 입력의 개수와 같은 가중치 존재. (모든 입력에 가중치를 곱하고 절편을 더한다.)
이미지와 같은 2차원 데이터를 1차원으로 펼쳐서 처리하기 때문에 비효율적

합성곱 convolution
가중치의 개수가 입력 개수와 다르다. (입력보다 작은 가중치) → 뉴런에 적은 가중치만 사용
뉴런X → 커널=필터=가중치

2차원 합성곱
이미지와 같은 2차원 데이터 특징 반영 가능
1차원과 마찬가지로 입력 수보다 적은 커널 사용

특성 맵 feature map
합성곱 계산을 통해 얻은 출력

2차원의 특성맵을 쌓아서 3차원의 배열로 구성이 될 수 있다.

패딩 padding
입력 주변에 한개의 픽셀을 덧붙이는 것
(보통 0으로 패딩하기 때문에 제로패딩이라고도 부름)
필터가 슬라이딩하는 면적을 넓힐 수 있다.
세임 패딩 (same padding) : 입력과 특성맵의 크기가 같아지게 만들 수 있음
밸리드 패딩 (valid padding) : 패딩 없이 순수 입력 배열만 사용. 특성 맵의 크기가 줄어듦.
패딩의 목적 : 가장자리에 있는 픽셀들은 패딩이 없으면 중앙에 있는 픽셀보다 적게 곱해져서 특성 반영이 적게 된다.

스트라이드 stride
필터를 이동하는 크기

풀링 pooling
특성 맵의 크기를 줄이는 역할 (특성 맵의 개수는 줄이지 않음)
(2, 2, 3) 특성 맵 → (1, 1, 3) 특성 맵으로 크기를 줄이는 것.
합성곱과 비슷하지만 가중치가 없음.
겹치지 않게 슬라이딩하는 것이 스트라이드와 다른 점.

합성곱 신경망의 구조
(4,4) 크기의 입력층
→ 패딩추가하여 (6,6) 크기로 변경
→ (3,3) 필터로 사용하여 (4,4) 특성 맵 3개 완성
→ (2,2) 풀링 적용하여 (2,2,3) 특성 맵 완성
→ 1차원으로 펼쳐서 출력층(밀집층)에 전달하여 최종 예측
중간단계를 여러번 거칠 수도 있다.

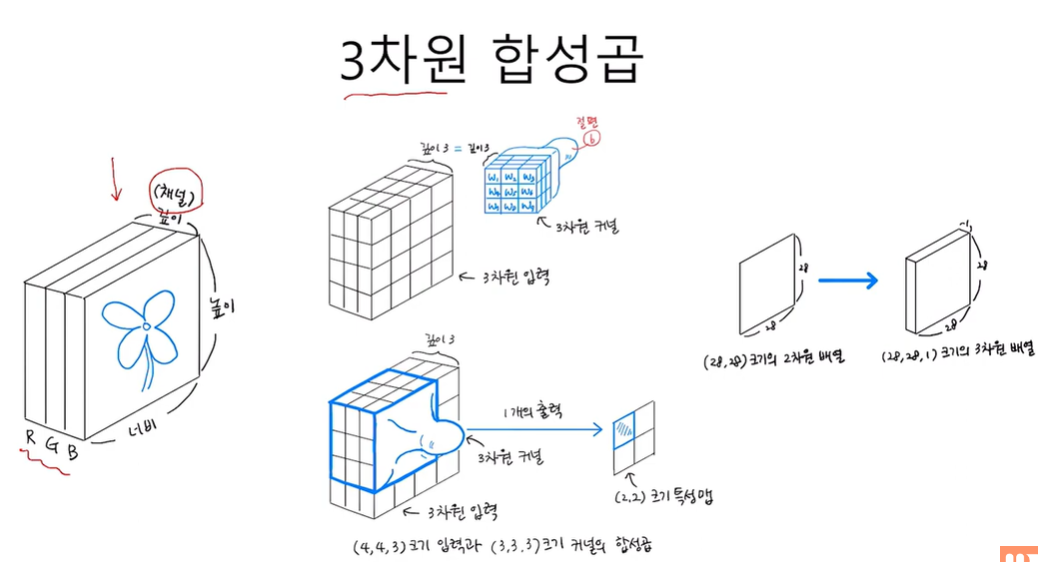
3차원 합성곱
입력의 깊이와 커널의 깊이를 같게 만든다.
8-2. 합성곱 신경망을 사용한 이미지 분류
# 패션 MNIST 데이터 불러오기
from tensorflow import keras
from sklearn.model_selection import train_test_split
(train_input, train_target), (test_input, test_target) = \
keras.datasets.fashion_mnist.load_data()
train_scaled = train_input.reshape(-1, 28, 28, 1) / 255.0 # 마지막 차원만 늘
train_scaled, val_scaled, train_target, val_target = train_test_split(
train_scaled, train_target, test_size=0.2, random_state=42)

# 합성곱 신경망 만들기
model = keras.Sequential()
# 첫번째 층 (필터 사이즈, 활성함수, 패딩)
model.add(keras.layers.Conv2D(32, kernel_size=3, activation='relu',padding='same', input_shape=(28,28,1)))
# 풀링 레이어 추가
model.add(keras.layers.MaxPooling2D(2))
model.add(keras.layers.Conv2D(64, kernel_size=(3,3), activation='relu',padding='same'))
model.add(keras.layers.MaxPooling2D(2))
model.add(keras.layers.Flatten())
model.add(keras.layers.Dense(100, activation='relu'))
model.add(keras.layers.Dropout(0.4))
model.add(keras.layers.Dense(10, activation='softmax'))
model.summary()
conv2d : 28x28x32 (입력크기 유지, 필터개수 32개)
max_pooling2d : 풀링을 통과하며 크기가 14로 절반으로 줄어듦
conv2d_1 : 합성곱 층을 한 번 더 수행하여 채널 수를 64개로 두배로 늘림
max_pooling2d_1 : 풀링을 한 번 더 통과하여 크기가 7로 다시 절반으로 줄임
flatten : 1차원으로 늘림
dense : 밀집층 처리

# 컴파일과 훈련
model.compile(optimizer='adam', loss='sparse_categorical_crossentropy', metrics=['accuracy'])
checkpoint_cb = keras.callbacks.ModelCheckpoint('best-model.keras', save_best_only=True)
early_stopping_cb = keras.callbacks.EarlyStopping(patience=2, restore_best_weights=True)
history = model.fit(train_scaled, train_target, epochs=20, verbose=0, validation_data=(val_scaled, val_target), callbacks=[checkpoint_cb, early_stopping_cb])
8-3. 합성곱 신경망 시각화

from tensorflow import keras
import matplotlib.pyplot as plt
model = keras.models.load_model('best-cnn-model.keras')
model.layers
# layers 속성에 sequentioal로 만들었던 층들을 파이썬 객체로 참조함 (8개의 층)
# layers에 있는 층 객체의 가중치를 확인
conv = model.layers[0]
print(conv.weights[0].shape, conv.weights[1].shape)
conv_weights = conv.weights[0].numpy()
print(conv_weights.mean(), conv_weights.std())
# 가중치 히스토그램으로 시각화하여 확인하기
plt.hist(conv_weights.reshape(-1, 1))
plt.xlabel('weight')
plt.ylabel('count')
plt.show()
# 커널 시각화
fig, axs = plt.subplots(2, 16, figsize=(15,2))
for i in range(2):
for j in range(16):
axs[i, j].imshow(conv_weights[:,:,0,i*16 + j], vmin=-0.5, vmax=0.5)
axs[i, j].axis('off')
plt.show()
훈련하지 않은 빈 합성곱 신경망의 가중치와 커널 시각화 결과


→ 훈련된 것보다 고르고 밋밋한 분포를 보임. (텐서플로가 가중치를 처음 초기화할 때 균등 분포에서 랜덤하게 값을 선택하기 때문)
⇒ 합성곱 신경망이 데이터셋 (패션 MNIST) 분류 정확도를 높이기 위해 패턴을 학습함.
함수형 API
입력과 출력이 여러개 등 복잡한 모델은 Sequential 클래스가 아닌 함수형 API를 사용
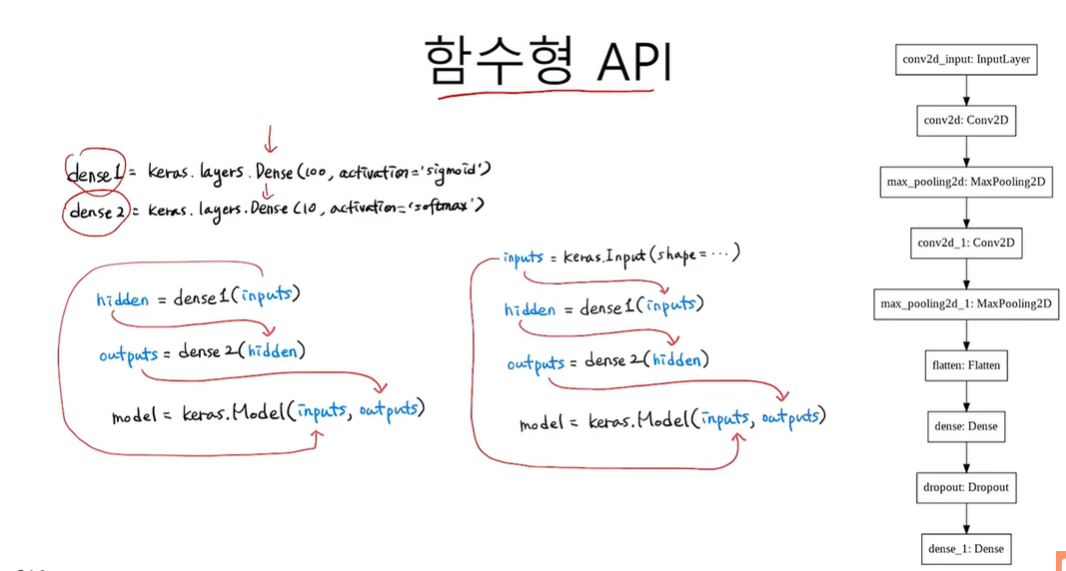
# 함수형 API
print(model.inputs) # input = 케라스에 있는 함수(클래스)
# [<KerasTensor shape=(None, 28, 28, 1), dtype=float32, sparse=False, name=input_layer>]
conv_acti = keras.Model(model.inputs, model.layers[0].output)
# conv_acti라는 새로운 모델 생성 (모델의 중간부분의 input과 output을 볼 수 있도록 만듦)(train_input, train_target), (test_input, test_target) = keras.datasets.fashion_mnist.load_data()
# 첫 번째 샘플
plt.imshow(train_input[0], cmap='gray_r')
plt.show()
# 첫 번째 특성 맵 시각화
# 전처리
inputs = train_input[0:1].reshape(-1, 28, 28, 1)/255.0
feature_maps = conv_acti.predict(inputs)
# 시각화
fig, axs = plt.subplots(4, 8, figsize=(15,8))
for i in range(4):
for j in range(8):
axs[i, j].imshow(feature_maps[0,:,:,i*8 + j])
axs[i, j].axis('off')
plt.show()
→ 32개 필터로 입력 이미지에서 강하게 활성화된 부분 보여짐.
# 두 번째 특성 맵 시각화
conv2_acti = keras.Model(model.inputs, model.layers[2].output)
feature_maps = conv2_acti.predict(train_input[0:1].reshape(-1, 28, 28, 1)/255.0)
fig, axs = plt.subplots(8, 8, figsize=(12,12))
for i in range(8):
for j in range(8):
axs[i, j].imshow(feature_maps[0,:,:,i*8 + j])
axs[i, j].axis('off')
plt.show()
→ 64개의 필터를 거친 특성 맵
층이 깊어지면서 직관적으로 이해하기 어려움. (어떤 부분을 감지하는지 알기 어려움)
참고자료:
1. 혼자 공부하는 머신러닝, 박해선, 한빛미디어
2. 혼자 공부하는 머신러닝 인프런 강의, 박해선, https://www.inflearn.com/course/%ED%98%BC%EC%9E%90%EA%B3%B5%EB%B6%80-%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EB%94%A5%EB%9F%AC%EB%8B%9D/dashboard
'Group Study (2024-2025) > Machine Learning 입문' 카테고리의 다른 글
| [ML 입문] 8주차 스터디 (1) | 2024.11.27 |
|---|---|
| [ML 입문] 6주차 스터디 (3) | 2024.11.10 |
| [ML 입문] 5주차 스터디 (1) | 2024.11.06 |
| [ML 입문] 4주차 스터디 (0) | 2024.10.30 |
| [ML 입문] 3주차 스터디 (1) | 2024.10.16 |